INVERSE PROPERTY OF MULTIPLICATION

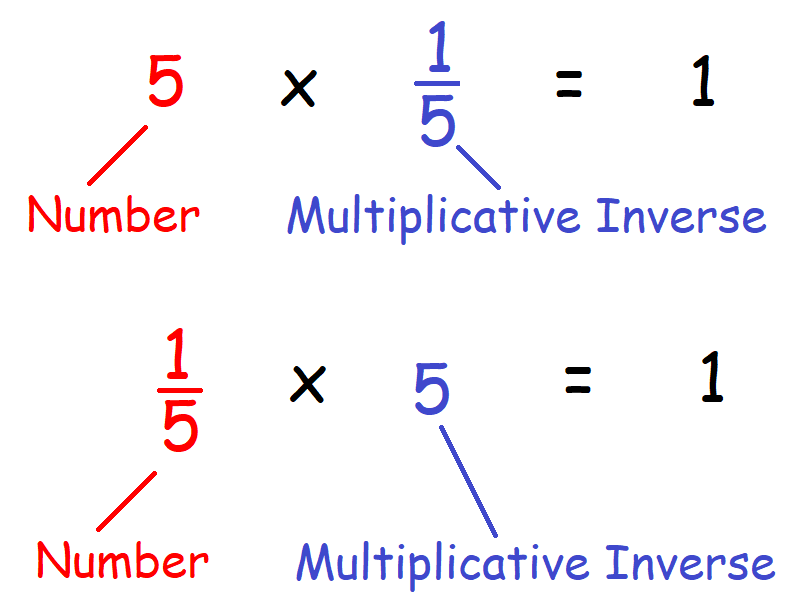
Words :

The product of a non zero real number and its reciprocal  or multiplicative inverse is 1.

Numbers :

3 ⋅ (1/3)  =  (1/3) ⋅ 3  =  1

-7 ⋅ (-1/7)  =  (-1/7) ⋅ (-7)  =  1

Algebra :

For any real number k (k ≠ 0),

k ⋅ (1/k)  =  (1/k) ⋅ k  =  1

Note :

To divide by a number, you can multiply by its multiplicative inverse.  

Problem 1 :

Verify whether 0.2 and 5 are multiplicative inverse to each other.  

Solution :

If 0.2 and 5 are multiplicative inverse to each other, their product has to be 1. 

0.2 x 5  =  (1/5) x 5

=  1

Because the product is 1, 0.2 and 5 are multiplicative inverse to each other. 

Problem 2 : 

If a and b are multiplicative inverse to each other, find a in terms of b. 

Solution :

Because a and b are multiplicative inverse to each other, their product is 1. 

ab  =  1

Solve for a : Divide each side by b. 

a  =  1/b

Problem 3 : 

If (y + 5) and 1/7 are multiplicative inverse to each other, find the value of y. 

Solution :

Because (y + 5) and 1/7 are multiplicative inverse to each other, their product is 1. 

(y + 5) ⋅ 1/7  =  1

(y + 5) / 7  =  1

Multiply each side by 7.

y + 5  =  7

Subtract 5 from each side. 

y  =  2

Problem 4 : 

If p + q  =  5/2, p and q are multiplicative inverses, find the value of p. 

Solution :

p + q  =  5/2

Subtract p from each side. 

q  =  5/2 - p

q  =  5/2 - 2p/2

q  =  (5 - 2p)/2

Because p and q are multiplicative inverses, their product is 1. 

pq  =  1

Substitute (5 - 2p)/2 for q. 

p ⋅ (5 - 2p)/2  =  1

[p(5 - 2p)] / 2  =  1

Multiply each side by 2.

5p - 2p²  =  2

Subtract 2 from each side. 

5p - 2p² - 2  =  0

-2p² + 5p - 2  =  0

Multiply each side by -1.

2p² - 5p + 2  =  0

Solve for p by factoring. 

2p² - p - 4p + 2  =  0

p(2p - 1) - 2(2p - 1) = 0

(2p - 1)(p - 2)  =  0

2p - 1  =  0  or  p - 2  =  0

p  =  1/2  or  p  =  2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.