LAW OF SINES or SINE FORMULA

The  Law of Sines is a relationship between the angles and the sides of a triangle. While solving a triangle, the law of sines can be effectively used in the following situations :

(i) To find an angle if two sides and one angle which is not included, by them are given.

(ii) To find a side, if two angles and one side which is opposite to one of given angles, are given.

Theorem (Law of Sines) :

In any triangle, the lengths of the sides are proportional to the sines of the opposite angles.

That is, in ΔABC,

where R is the circumradius of the triangle.

Proof :

The angle A of the ΔABC is either acute or obtuse or right. Let O be the center of the circumcircle ΔABC and R, its radius

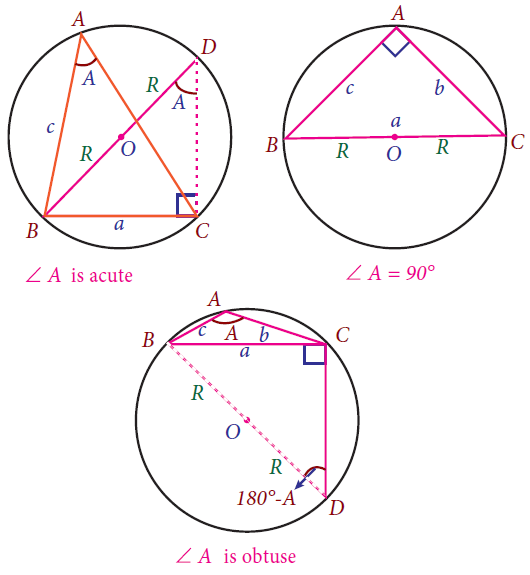
Case (i) : ∠A is acute.

Produce BO to meet the circle at D.

∠BDC = ∠BAC = A

∠BCD = 90°

sin∠BDC = BC/BD

sinA = a/2R

a/sinA = 2R

Case (ii) : ∠A is right angle.

In this case, O must be on the side BC of the ΔABC

Now, 

a/sinA = BC/sin90°

a/sinA = 2R/1

a/sinA = 2R

Case (iii) : ∠A is obtuse.

Produce BO to meet the circle at D.

∠BDC + ∠BAC = 180°

∠BDC = 180° - ∠BAC

∠BDC = 180° - A

∠BCD = 90°

sin∠BDC = BC/BD

sin(180° - A) = a/2R

sinA = a/2R

a/sinA = 2R

In each case, we have

Similarly, by considering angles B and C, we can prove that

respectively.

Thus,

Remarks

1. The Law of Sines can be written as a collection of three equations.

2. The Law of Sines says that the sides of a triangle are proportional to the sines of their opposite angles.

3. Using the Law of Sines, it is impossible to find the solution to a triangle given two sides and the included angle.

4. An interesting geometric consequence of the Law of Sines is that the largest side of any triangle is opposite to the largest angle.

Solving Problems Using Law of Sines

Problem 1 :

In a triangle ABC, if a = 2, b = 3 and sinA = 2/3, find ∠B.

Solution :

Using Law of Sines,

a/sinA = b/sinB

Substitute.

2/(2/3) = 3/sinB

3 = 3/sinB

3sinB = 3

sinB = 1

∠B = 90°

Problem 2

If the angles of a triangle are in the ratio 1 : 2 : 3, prove that the corresponding sides are in the ratio 1 : √3 : 2.

Solution :

From the ratio 1 : 2 : 3, the angles of a triangle are assumed to be x, 2x and 3x.

x + 2x + 3x = 180°

6x = 180°

x = 30°

So, the angles are 30°, 60° and 90°.

Let a, b and c be the corresponding side lengths of the angles 30°, 60° and 90° respectively.

Using Law of Sines,

a/sin30° = b/sin60° = c/sin90°

Let a/sin30° = b/sin60° = c/sin90° = k.

a : b : c = k/2 : k√3/2 : k

= k : k√3 : 2k

= 1 : √3 : 2

Problem 3 :

The angles of a triangle ABC are in arithmetic sequence If b/c = √3/√2, find ∠A.

Solution :

It is given that the angles ∠A, ∠B and ∠C are in arithmetic sequence.

∠B -  ∠A = ∠C - ∠B

2∠B = ∠A + ∠C ----(1)

Add ∠B to both sides.

3∠B = ∠A + ∠B + ∠C

3∠B = 180°

∠B = 60°

Using Law of Sines,

In (1), substitute ∠B = 60° and ∠C = 45° and solve for ∠A.

2∠B = ∠A + ∠C

2(60°) = ∠A + 45°

120° = ∠A + 45°

75° = ∠A

Problem 4 :

If in a triangle ABC, ∠A = 45°, ∠B = 60° and ∠C = 75°, find the ratio of its sides.

Solution :

Law of Sines :

a/sinA = b/sinB = c/sinC

a/sin45° = b/sin60° = c/sin75°

Let a/sin45° = b/sin60° = c/sin75° = k

Find the value of sin75°.

sin75° = sin(45° + 30°)

= sin(45° + 30°)

= sin45°cos30° + cos45°sin30°

Problem 5 :

In ΔABC, ∠B = 45°, ∠C = 105° and a = 2, find b.

Solution :

In ΔABC,

∠A + ∠B + ∠C = 180°

∠A + 45° + 105° = 180°

∠A + 150° = 180°

∠A = 30°

By Law of Sines :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.