LINEAR FUNCTIONS

The graph shown below represents a function, because each domain value (x-value) is paired with exactly one range value (y-value).

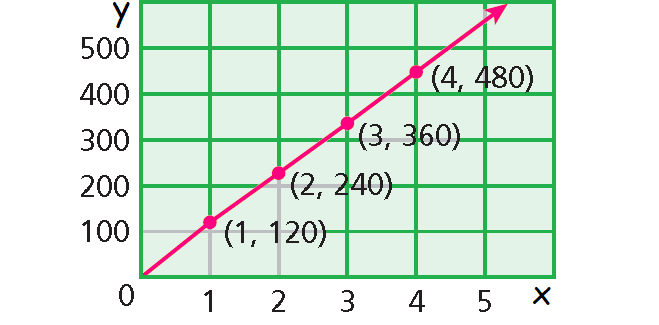
Notice that the graph is a straight line. A function whose graph forms a straight line is called a linear function.

Identifying a Linear Function by Its Graph

Identify whether each graph represents a function. Explain. If the graph does represent a function, is the function linear?

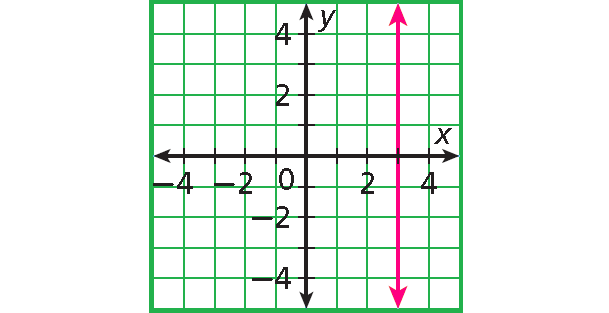
Example 1 : 

Solution : 

Each domain value is paired with exactly one range value. The graph forms a line.

linear function

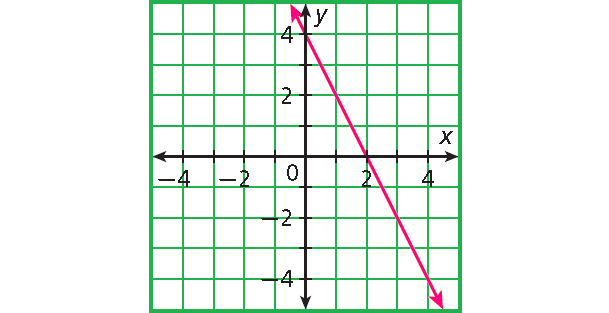
Example 2 : 

Solution : 

Each domain value is paired with exactly one range value. The graph is not a line.

not a linear function

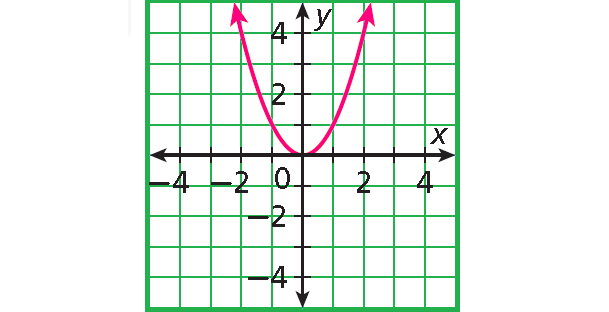
Example 3 : 

Solution : 

The only domain value, 3, is paired with many different range values.

not a function

Identifying a Linear Function by Using Ordered Pairs

You can sometimes identify a linear function by looking at a table or a list of ordered pairs. In a linear function, a constant change in x corresponds to a constant change in y.

Tell whether each set of ordered pairs satisfies a linear function. Explain.

Example 4 : 

{(2, 4), (5, 3), (8, 2), (11, 1)}

Solution : 

Write the ordered pairs in a table and look for a pattern.

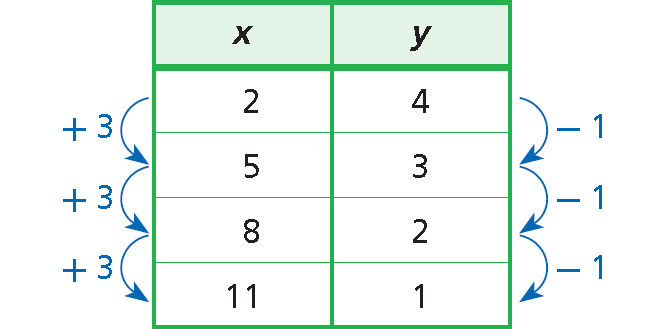
A constant change of +3 in x corresponds to a constant change of -1 in y.

These points satisfy a linear function.

Example 5 : 

{(-10, 10), (-5, 4), (0, 2), (5, 0)}

Solution : 

Write the ordered pairs in a table and look for a pattern.

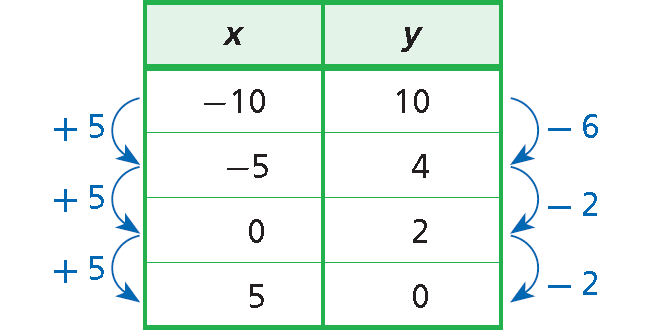
A constant change of +5 in x corresponds to different changes in y.

These points do not satisfy a linear function.

Linear Equation

Another way to determine whether a function is linear is to look at its equation. A function is linear if it is described by a linear equation. A linear equation is any equation that can be written in the standard form shown below.

Standard Form of a Linear Equation

Ax + By  =  C

where A, B, and C are real numbers and A and B are not both 0. 

Notice that when a linear equation is written in standard form

• x and y both have exponents of 1.

• x and y are not multiplied together.

• x and y do not appear in denominators, exponents, or radical signs.

For any two points, there is exactly one line that contains them both. This means you need only two ordered pairs to graph a line.

Graphing Linear Functions

Tell whether each function is linear. If so, graph the function.

Example 6 : 

y  =  x + 3

Solution : 

y  =  x + 3

Write the equation in standard form.

Subtract x from each side. 

-x + y  =  3

The equation is in standard form (A = -1, B = 1, C = 3).

The equation can be written in standard form, so the function is linear.

To graph, choose three values of x, and use them to generate ordered pairs. (You only need two, but graphing three points is a good check.)

Plot the points and connect them with a straight line.

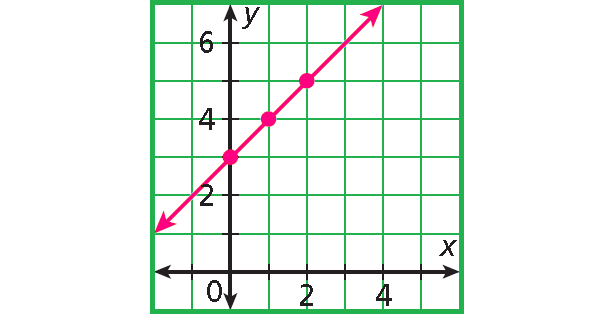
Example 7 : 

y  =  x²

Solution : 

y  =  x²

This is not linear, because x has an exponent other than 1.

Career Application

Example 8 :

Lily rents a manicure station in a salon and pays the salon owner $5.50 for each manicure she gives. The amount Lily pays each day is given by f (x) = 5.50x, where x is the number of manicures. Graph this function and give its domain and range.

Solution : 

Choose several values of x and make a table of ordered pairs.

Graph the ordered pairs.

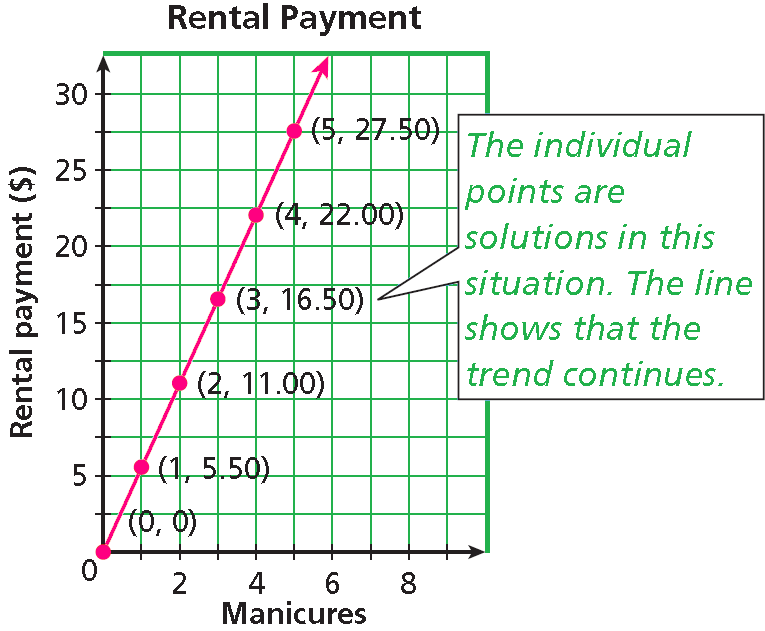
The number of manicures must be a whole number, so the domain is

{0, 1, 2, 3, .......}

The range is

{0, 5.50, 11.00, 16.50, .......}

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.