MARKUP AND MARKDOWN WORD PROBLEMS WORKSHEET

1) A golf store pays its wholesaler $40 for a certain club, and then sells it to a golfer for $75. What is the markup rate?

2) A product is originally priced at $55 is marked 25% off. What is the sale price?

3) A product is marked down 15%; the sale price is $127.46. What was the original price?

4) A sells to B an item at 15% profit. B sells the same item to C at 20% profit. If C pays $1656 for it. What is the price at which A bought the item?

5) If good are purchased for $ 1500 and one fifth of them sold at a loss of 15%. Then at what mark up rate should the rest be sold to obtain a overall mark up rate of 15%?

6) By selling 20 articles, a trader gained the selling price of 5 articles. Find the mark up rate.  

7) A person wants to get 20% mark up rate after selling his object at 20% discount. Find the required percentage increase in marked price. 

8) The selling price of 10 articles is the cost price of 15 articles. Find profit or loss percentage. 

9) On selling 20 units of an item, the profit is equal to cost price of 5 units. Find the mark mark up rate.

10) Difference between the cost price of two products is $10. Difference between the selling price is $20. If one is sold at 20% profit and other one is sold at 20% loss, find the cost price of each product.  

Detailed Answer Key

Answer (1) : 

Cost price (C.P)  =  $40

Selling price (S.P)  =  $75

Mark up value  =  75 - 40  =  $35

Mark up rate  =  (35 / 40) ⋅ 100%  =  87.5%

So, the mark up rate is 87.5 %

Answer (2) : 

Selling price (S.P)  =  (100 - m)% ⋅ L.P -----(1)

Here,

L.P  =  $55,  m  =  25    

Substitute 55 for L.P and 25 for m in (1). 

(1)----->  S.P  =  (100 - 25)% ⋅ 55 

S.P  =  75% ⋅ 55

S.P  =  0.75 ⋅ 55

S.P  =  41.25

So, the selling price is $ 41.25.

Answer (3) : 

Selling price (S.P)  =  (100 - m)% ⋅ Original price -----(1)

Here,  

S.P  =  127.46,  m  =  15

Substitute 127.46 for S.P and 15 for m in (1). 

127.46  =  (100 - 15)% ⋅ Original price

127.46  =  85% ⋅ Original price 

127.46  =  0.85 ⋅ Original price

127.46 / 0.85  =  Original price 

149.95  =  Original price 

So, the original price is $ 149.95.

Answer (4) :

Let x be the cost price of A. 

Then, we have

Cost price of B  =  1.15x

Cost price of C  =  1.2(1.15x)

Cost price of C  =  1.38x

Given : The cost of C is $1656.

1.38x  =  1656

Divide each side by 1.38

x  =  1200

So, the price at which A bought the item is $1200. 

Answer (5) :

As per the question, we need 15% mark up rate on $1500.

Selling price for 15% on 1500 :

S.P  =  115% ⋅ 1500

S.P  =  1.15 ⋅ 1500

S.P  =  1725

When all the good sold, we must have received $1725 for 15% mark up rate.

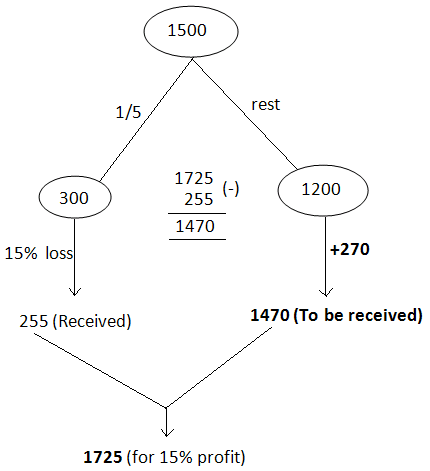
When we look at the above picture, in order to reach 15% mark up rate overall, the rest of the goods ($1200) has to be sold for $1470.

That is,

C.P  =  $1200

S.P  =  $1470

Profit  =  $270

Mark up rate  =  (270 / 1200) ⋅ 100%

Mark up rate  =  22.5%

So, the rest of the goods to be sold at the mark up rate of 22.5% in order to have the mark up rate of 15% overall.

Answer (6) :

Let x be the S.P of 5 articles.

Given : Profit of 20 articles is S.P of 5 articles

Then, profit of 20 articles is x.

S.P of 20 articles  =  4(S.P of 5 articles)

S.P of 20 articles  =  4x

C.P of 20 art.  =  S.P of 20 art. - Profit of 20 art.

C.P of 20 articles  =  4x - x

C.P of 20 articles  =  3x

Mark up rate  =  (x / 3x) ⋅ 100%

Mark up rate  =  (1/3) ⋅ 100%

Mark up rate  =  33.33%

Answer (7) :

Let the cost price be $100. 

Then, the selling price is $120.

Let x be the marked price. 

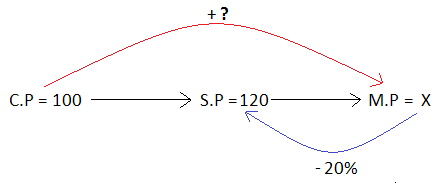
From the above picture, we get

80% of (M.P)  =  S.P

(0.8)x  =  120

x  =  150

Therefore, the marked price is $150. 

Cost price  =  $100

Marked Price  =  $150

So, the required percentage increase is 50%.

Answer (8) :

Let the cost price of one article be $1 -----(1) 

Given : The selling price of 10 articles is the cost price of 15 articles. 

Then, we have

S.P of 10 articles  =  15 ⋅ 1  =  $15

S.P of one article  =  15 / 10  =  $1.5 -----(2)

From (1) and (2), the selling price is more than the  cost price.

That is, S.P > C.P

So, there is profit.

Profit  =  (2) - (1)

Profit  =  1.5 - 1

Profit  =  0.5

Profit percentage  =  (0.5 / 1) ⋅ 100  =  50%

So, the profit percentage  =  50%.

Answer (9) :

Let m be the cost price of one unit. 

Then, we have

Cost price of 5 units  =  5m

Cost price of 20 units  =  20m

Given : On selling 20 units of an item, the profit is equal to cost price of 5 units.

Then, we have

Profit  on selling 20 units  =  C.P of 5 units  =  5m 

Mark up rate  =  (profit / cost) ⋅ 100%

Mark up rate  =  (5m / 20m) ⋅ 100%

Mark up rate  =  (1 / 4) ⋅ 100%

Mark up rate  =  25%

Answer (10) :

Let x and y be the cost prices of two products. 

Then, we have

x - y  =  10 -----(1)

Let us assume that x is sold at 20% profit.

Then, the selling price of x is

=  120% ⋅ x

=  1.2x

Let us assume that y is sold at 20% loss. 

Then, the selling price of y is

=  80% ⋅ y

=  0.8y

Given : Difference between the selling price is $20

1.2x - 0.8y  =  20

Multiply each side by 10.

12x - 8y  =  200

Divide each side by 4.

3x - 2y  =  50 -----(2)

Solving (1) and (2), we get

x  =  30

y  =  20 

So, the cost prices of the two products are $30 and $20.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.