MIXED QUESTIONS ON MEAN MEDIAN AND MODE FOR UNGROUPED DATA

Question 1 :

The monthly salary (in $) of 10 employees in a factory are given below :

5000, 7000, 5000, 7000, 8000, 7000, 7000, 8000, 7000, 5000

Find the mean, median and mode.

Solution : 

Mean :

= (5000 + 7000 +  5000 + 7000 + 8000 + 7000 + 7000 + 8000 + 7000 + 5000)/10

  =  66000/10

  =  6600

Median :

5000, 5000, 5000, 7000, 7000, 7000, 7000, 7000,  8000, 8000

Number of observations  =  10 (Even)

Median  =  {(10/2)^th observation + [(10/2) + 1]^th}/2

  =  (5^th observation + 6^th observation)/2

  =  (7000 + 7000)/2

  =  14000/2

  =  7000

Mode :

7000 is repeating 5 times. Hence mode is 7000.

Question 2 :

Find the mode of the given data : 3.1, 3.2, 3.3, 2.1, 1.3, 3.3, 3.1

Solution :

3.1 and 3.3 are repeating twice, so mode is 3.1 and 3.3

It is a bimodal data.

Question 3 :

For the data 11, 15, 17, x+1, 19, x–2, 3 if the mean is 14 , find the value of x. Also find the mode of the data.

Solution :

Mean  =  (11 + 15 + 17 + x + 1 + 19 + x - 2 + 3)/7

14  =  (64 + 2x)/7

14(7)  =  64 + 2x

2x  =  98 - 64

2x  =  34

x  =  34/2  =  17

By applying the value of x in the given observation, we get 

11, 15, 17, 18, 19, 15, 3

Mode  =  15 (Repeating twice)

Question 4 :

The demand of track suit of different sizes as obtained by a survey is given below:

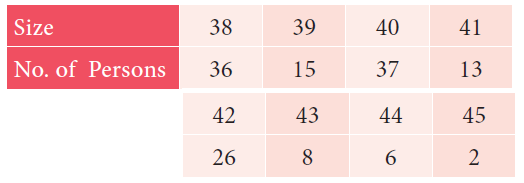
Solution :

Demand for the size 40 is 37.

Hence the demand of size 40 is high.

Steps in Finding the Mode of Grouped Data

In case of a grouped frequency distribution, the exact values of the variables are not known and as such it is very difficult to locate mode accurately

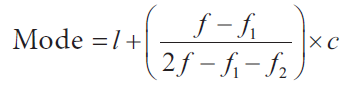
The class interval with maximum frequency is called the modal class.

Where l - lower limit of the modal class;

f - frequency of the modal class

f1 - frequency of the class just preceding the modal class

f2 - frequency of the class succeeding the modal class

c - width of the class interval

Question 5 :

Find the mode of the following data:

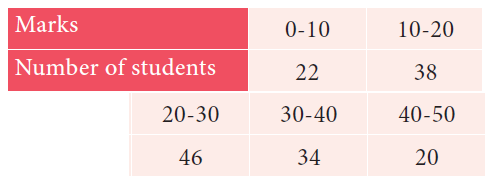
Solution :

The highest frequency is 46

modal class is 20 - 30

l = 20, f = 46, f1 = 38, f2 = 34, c = 10

  =  20 + [(46-38)/2(46) - 38 - 34] x 10

  =  20 + [8/(92 - 38 - 34)] x 10

  =  20 + [8/20] x 10

  =  20 + 4

  =  24

Hence the mode is 24.

Question 6 :

Find the mode of the following distribution:

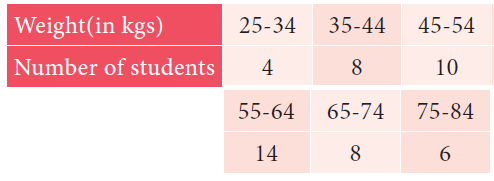
Solution :

The highest frequency is 14

modal class is 54.5 - 64.5

l = 54.5, f = 14, f1 = 10, f2 = 8, c = 10

  =  54.5 + [(14 - 10)/2(14) - 10 - 8] x 10

  =  54.5 + [4/(28 - 18)] x 10

  =  54.5 + [4/10] x 10

  =  54.5 + 4

  =  58.5

Hence the mode is 58.5.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.