MODELING GEOMETRIC FIGURES

When it comes to using geometry to solve real-world problems, we will learn how modeling our real-world problem with a common geometric shape can help us to easily solve the problem.

Example 1 : 

Peter’s blueprint given below shows a layout of a house. Every 4 inches in the blueprint represents 3 feet of the actual house. One of the walls in the blueprint is 24 inches long. What is the actual length of the wall ?

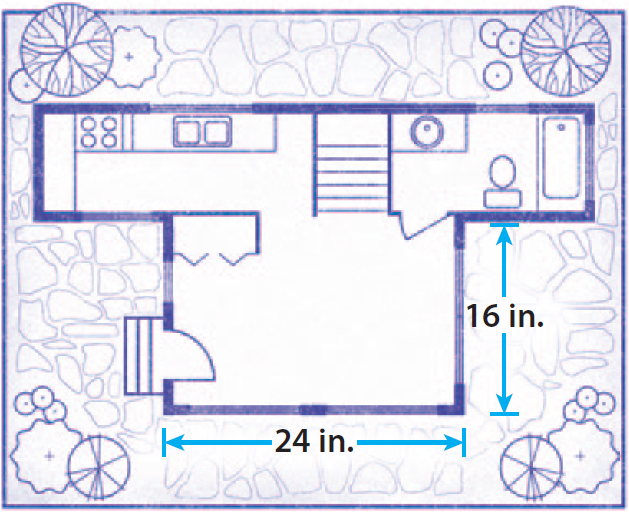
Solution : 

Let "x" be the original length of the wall in feet. 

Step 1 :

Using scale factor, we have 

4 inches -----> 3 feet 

24 inches -----> x feet

Step 2 :

Let us proportion to solve for "x" 

4 : 3  =  24 : x

or

4/3  =  24/x

Step 3 : 

Simplify

4x  =  (24)(3)

x  =  (24)(3) / 4

x  =  (6)(3)

x  =  18

So, the original length of the wall is 18 feet.

Example 2 : 

David would like to make paint the rectangular shaped wall. The measures of dimensions of the wall is given in the picture using scale factor. In the picture given below, every 1 inch represents 3 feet of the actual length. If the cost of painting is $2.50 per square feet, find the total cost of painting for the entire wall. 

Solution : 

Scale factor : 1 in = 3 feet

Step 1 :

Find the length of the wall in feet. 

Length  =  8 inches

Length  =  8 x 3 feet

Length  =  24 feet

Step 2 :

Find the width of the wall in feet. 

Width  =  4 inches

Width  =  4 x 3 feet

Width  =  12 feet

Step 3 : 

Find area of the wall in square feet. 

Area of the wall  =  Length x Width 

Area of the wall  =  24 x 12

Area of the wall  =  288 square feet.  

Step 4 : 

Find the total cost of painting for the entire wall. 

Cost of painting per square feet  =  $2.50

Total cost of painting for the entire wall  is equal to area of the wall times $2.50

=  288 x 2.50

=  720

So, the total cost of painting for the entire wall is $720

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.