MULTIPLE REPRESENTATIONS OF RELATIONS

Relations can be represented in multiple ways, such as tables, graphs, or mapping diagrams.

Example 1 : 

In the scoring system of some track meets, first place is worth 5 points, second place is worth 3 points, third place is worth 2 points, and fourth place is worth 1 point. This scoring system is a relation, so it can be shown as ordered pairs, {(1, 5), (2, 3), (3, 2), (4, 1)}. Express the relation for the track meet scoring system as a table, as a graph, and as a mapping diagram.

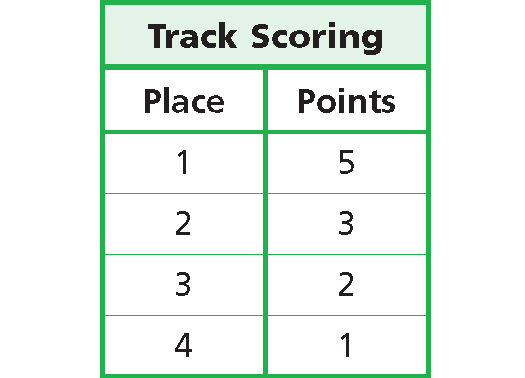
Table : 

Write all x-values under “Place” and all y-values under “Points.”

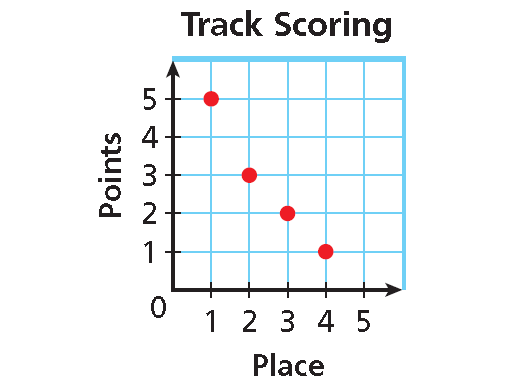
Graph : 

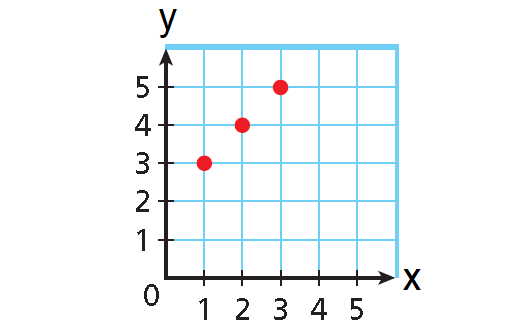
Use the x- and y-values to plot the ordered pairs.

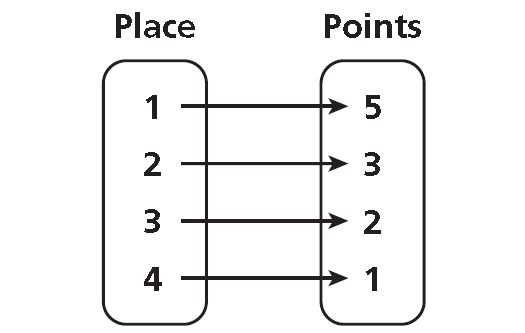
Mapping Diagram : 

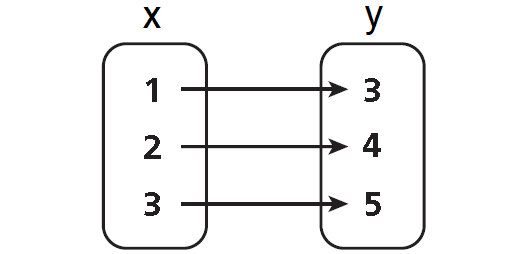
Write all x-values under “Place” and all y-values under “Points.” Draw an arrow from each x-value to its corresponding y-value.

Example 2 : 

Express the relation {(1, 3), (2, 4), (3, 5)} as a table, as a graph, and as a mapping diagram.

Table : 

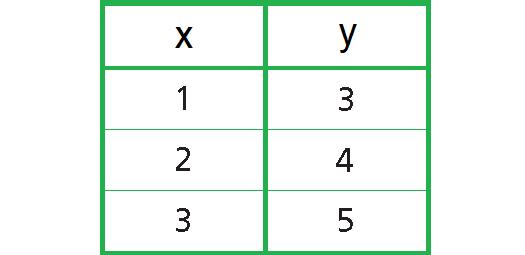
Graph : 

Mapping Diagram : 

For each of the examples state the domain and range of the relations.

Example 3 : 

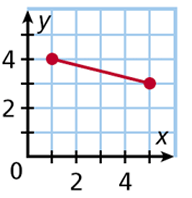
Solution :

The relation is represented as graph, in the graph the relation horizontally starts at 1 and ends at 5.

By observing the graph vertically, it starts at 3 and ends at 4.

Domain = [1, 5]

Range = [3, 4]

Example 4 : 

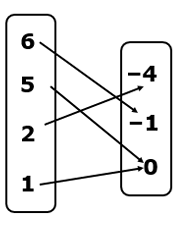
Solution :

The relation is represented as arrow diagram, all inputs are domain and all outputs are range.

Domain = {6, 5, 2, 1}

Range = {-4, -1, 0}

Example 5 : 

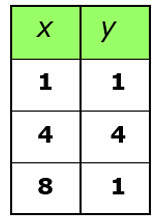
Solution :

The relation is represented as table, all values of x are domain and all values of y are range.

Domain = {1, 4, 8}

Range = {1, 4}

Since 1 is repeating two times, it is enough write it once.

Example 6 : 

Give the domain and range of the relation. Tell whether the relation is a function. Explain.

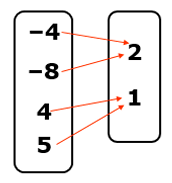
Solution :

Domain = {-4, -8, 4, 5}

Range = {1, 2}

Every input is associated with one output. So, it is a function.

Express each relation as table, as a graph and as mapping.

Example 7 :

{(-5, 3) (-2, 1) (1, -1) (4, -3)}

Solution :

To represent in the table, we have to observe the set of ordered pairs and write the first values as x and second values as y.

If any value is repeating, write it down once.

As table :

As graph :

Representing set of ordered pairs in coordinate plane, we get

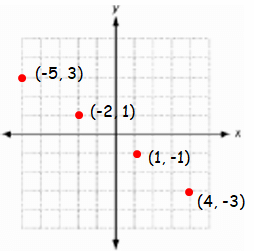
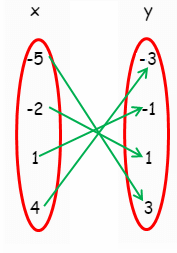
As mapping :

From the relation, {(-5, 3) (-2, 1) (1, -1) (4, -3)} we know that 

• -5 is associated with 3
• -2 is associated with 1
• 1 is associated with -1 
• 4 is associated with -3

Example 8 :

{(4, 0) (4, 1) (4, 2) (4, 4) (4, 5)}

Solution :

To represent in the table, we have to observe the set of ordered pairs and write the first values as x and second values as y.

If any value is repeating, write it down once.

As table :

As graph :

Representing set of ordered pairs in coordinate plane, we get

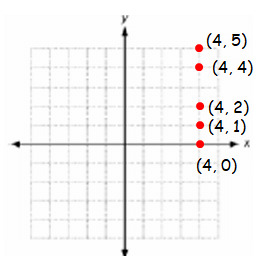
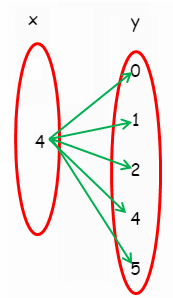
As mapping :

From the relation, {(4, 0) (4, 1) (4, 2) (4, 4) (4, 5)} we know that 

• 4 is associated with 0
• 4 is associated with 1
• 4 is associated with 2
• 4 is associated with 4
• 4 is associated with 5

Give the domain and range of each relation, tell whether the relation is a function. Explain.

Example 9 :

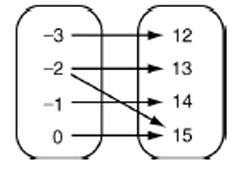
Solution :

Domain = {-3, -2, -1, 0}

Range = {12, 13, 14, 15}

The above relation is not a function, because -2 is having more than one image. So, it is not a function.

Example 10 :

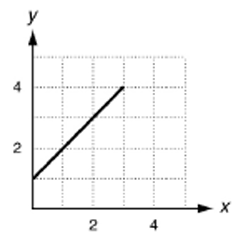
Solution :

Domain = [1, 3]

Range = [0, 4]

The above relation is s function, by using vertical line test. Drawing a vertical line, it will intersect the given curve at one point maximum. So, it is function.

Example 11 :

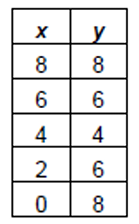
Solution :

Domain = {0, 2, 4, 6, 8}

Range = {4, 6, 8}

By observing all inputs, no input is having more than one outputs. So, it is a function.

Example 12 :

Write a function to describe the situation. Find a reasonable domain and range of the function. Joe has enough money to buy 1, 2 or 3 DVDs at $15 each.

Solution :

Let x be the number of DVDs.

f(x) be the cost to buy DVDs.

Cost of one DVD = 15

f(x) = 15x

When x = 1, f(1) = 15(1) ==> 15

When x = 2, f(2) = 15(2) ==> 30

When x = 3, f(3) = 15(3) ==> 45

Domain = {1, 2, 3}

Range = {15, 30, 45}

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.