MULTIPLICATION OF COMPLEX NUMBERS

To multiply the complex numbers, we can use the distributive multiplication method.

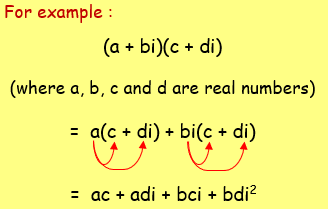
Since i²  =  -1

=  ac + adi + bci + bd(-1)

=  ac + adi + bci – bd

=  ac – bd + (ad + bc)i

Write the product in standard form :

Example 1 :

(2 + 3i)(2 – i)

Solution :

(2 + 3i)(2 – i)  =  2(2) – 2(i) + 3i(2) – 3i(i)

=  4 – 2i + 6i – 3i²

=  4 + 4i – 3(-1)

=  4 + 4i + 3

=  7 + 4i

So, the standard form is 7 + 4i

Example 2 :

(2 - i)(1 + 3i)

Solution :

(2 - i)(1 + 3i)  =  2(1) + 2(3i) - i(1) – i(3i)

=  2 + 6i - i – 3i²

=  2 + 5i – 3(-1)

=  2 + 5i + 3

=  5 + 5i

So, the standard form is 5 + 5i

Example 3 :

(1 - 4i)(3 - 2i)

Solution :

(1 - 4i)(3 - 2i)  =  1(3) – 1(2i) - 4i(3) + 4i(2i)

=  3 - 2i - 12i + 8i²

=  3 - 14i + 8(-1)

=  3 - 14i - 8

=  -5 - 14i

So, the standard form is -5 - 14i

Example 4 :

(5i - 3)(2i + 1)

Solution :

(5i - 3)(2i + 1)  =  5i(2i) + 5i(1) - 3(2i) - 3(1)

=  10i² + 5i - 6i - 3

=  10(-1) + 5i – 6i - 3

=  -10 + 5i – 6i - 3

=  -13 - i

So, the standard form is -13 – i

Example 5 :

(7i - 3)(2 + 6i)

Solution :

(7i - 3)(2 + 6i)  =  7i(2) + 7i(6i) - 3(2) - 3(6i)

=  14i + 42i² - 6 – 18i

=  14i + 42(-1) – 6 – 18i

=  -4i - 42 – 6

=  -4i – 48

=  -48 – 4i

So, the standard form is -48 – 4i

Example 6 :

(√-4 + i)(6 - 5i)

Solution :

(√-4 + i)(6 - 5i)  =  √-4(6) - √-4(5i) + i(6) - i(5i)

=  6√-4 – 5i√-4 + 6i – 5i²

Since i  =  √-1

=  6i(2) - 5i(i)(2) + 6i – 5(-1)

=  12i – 10i² + 6i + 5

=  18i – 10(-1) + 5

=  18i + 10 + 5

=  18i + 15

=  15 + 18i

So, the standard form is 15 + 18i

Example 7 :

(-3 - 4i)(1 + 2i)

Solution :

(-3 - 4i)(1 + 2i)  =  -3(1) - 3(2i) - 4i(1) – 4i(2i)

=  -3 - 6i - 4i – 8i²

=  -3 - 10i – 8(-1)

=  -3 - 10i + 8

=  5 - 10i

So, the standard form is 5 - 10i

Example 8 :

(√-2 + 2i)(6 + 5i)

Solution :

(√-2 + 2i)(6 + 5i)  =  √-2(6) + √-2(5i) + 2i(6) + 2i(5i)

=  6√-2 + 5i√-2 + 12i + 10i²

Since i  =  √-1

=  6i√2 + 5i(i)√2 + 12i + 10(-1)

=  6√2i + 5√2i² + 12i - 10

=  6√2i + 5√2(-1) + 12i - 10

=  6√2i - 5√2 + 12i – 10

By combining like terms, we get

=  6√2i + 12i - 5√2 – 10

=  -5√2 – 10 + (6√2 + 12)i

So, the standard form is -5√2 – 10 + (6√2 + 12)i

Example 9 :

(3 + 3i)(1 + 4i)(−2 + 3i)

Solution :

(3 + 3i)(1 + 4i)(−2 + 3i)

(3 + 3i)(1 + 4i) = 3 + 12i + 3i + 12i²

= 3 + 15i + 12(-1)

= 3 + 15i - 12

= -9 + 15i

(3 + 3i)(1 + 4i)(−2 + 3i) = (-9 + 15i) (−2 + 3i)

= 18 - 27i - 30i + 45i²

= 18 - 45 - 3i

= -27 - 3i

Example 10 :

(4 + 3i)(−2 − 3i)(1 − i)

Solution :

= (4 + 3i)(−2 − 3i)(1 − i)

(4 + 3i)(−2 − 3i) = -8 - 6i - 6i - 9i²

= -8 - 12i + 9

= 1 - 12i

(4 + 3i)(−2 − 3i)(1 − i) = (1 - 12i)(1 - i)

= 1 - i - 12i + 12i²

= 1 - 13i + 12(-1)

= 1 - 12 - 13i

= -11 - 13i

Example 11 :

−3(−3 − 4i) + 3(−i)

Solution :

= −3(−3 − 4i) + 3(−i)

= 9 + 12i - 3i

= 9 + 9i

Example 12 :

(−3 − 4i)²

Solution :

= (−3 − 4i)²

= (3 + 4i)²

Looks like the formula (a + b)²

= a² + 2ab + b²

= 3² + 2(3)(4i) + (4i)²

= 9 + 24i - 16

= -7 + 24i

Example 13 :

−4(−5 − 2i) + 2(−3 + 5i)

Solution :

= −4(−5 − 2i) + 2(−3 + 5i)

Distributing -4 and 2, we get

= 20 + 8i - 6 + 10i

= 14 + 18i

Example 13 :

(5 + i)²

Solution :

(5 + i)²

(a + b)² = a² + 2ab + b²

= 5² + 2(5)i + i²

= 25 + 10i - 1

= 24 + 10i

Example 14 :

(5i)( −5 + i) + 4( 5 − i) 16) ( −2 + 5i)

Solution :

= (5i)( −5 + i) + 4(5 − i)

= -25i + 5i² + 20 - 4i

combining the like terms, we get

= -25i - 5 + 20 - 4i

= -29i + 15

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.