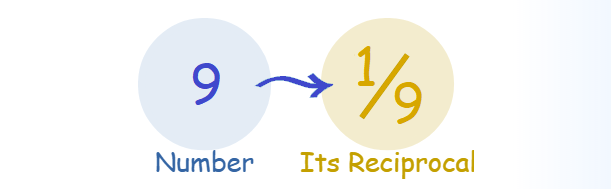
MULTIPLICATIVE INVERSE OR RECIPROCAL

If the product of two real numbers is 1, then they are reciprocals.

A number and its reciprocal are called multiplicative inverses.

For a real number 'y', its reciprocal '1/y' is its multiplicative inverse.

For '1/y', its reciprocal 'y' is its multiplicative inverse.  

Solved Problems

Problem 1 : 

If x and y are multiplicative inverse to each other, find x in terms of y. 

Solution : 

Because x and y are multiplicative inverse to each other, their product is 1. 

xy  =  1

Solve for x : Divide each side by y. 

x  =  1/y

Problem 2 : 

If (x + 3) and 1/5 are multiplicative inverse to each other, find the value of x. 

Solution : 

Because (x + 3) and 1/5 are multiplicative inverse to each other, their product is 1. 

(x + 3) ⋅ 1/5  =  1

(x + 3) / 5  =  1

Multiply each side by 5.

x + 3  =  5

Subtract 3 from each side. 

x  =  2

Problem 3 : 

If x + y  =  10/3, x and y are multiplicative inverses, find the value of x. 

Solution : 

x + y  =  10/3

Subtract x from each side. 

y  =  10/3 - x

y  =  10/3 - 3x/3

y  =  (10 - 3x)/3

Because x and y are multiplicative inverses, their product is 1. 

xy  =  1

Substitute (10 - 3x)/3 for y. 

x ⋅ (10 - 3x)/3  =  1

[x(10 - 3x)] / 3  =  1

Multiply each side by 3.

10x - 3x²  =  3

Subtract 3 from each side. 

10x - 3x² - 3  =  0

-3x² + 10x - 3  =  0

Multiply each side by -1.

3x² - 10x + 3  =  0

Solve for x by factoring. 

3x² - x - 9x + 3  =  0

x(3x - 1) - 3(3x - 1) = 0

(3x - 1)(x - 3)  =  0

3x - 1  =  0  or  x - 3  =  0

x  =  1/3  or  x  =  3

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.