MULTIPLYING MORE THAN TWO RATIONAL NUMBERS WORKSHEET

Problem 1 : 

Multiply (-2/3)(-1/2)(-3/5). 

Problem 2 : 

Multiply 1/6, 3/10 and -40. 

Problem 3 : 

Multiply -4, -4.5 and - 2. 

Problem 4 : 

Multiply -4, -2.5, 5 and - 1.4. 

Detailed Answer Key

Problem 1 : 

Multiply :

(-2/3)(-1/2)(-3/5)

Solution : 

Step 1 : 

First, find the product of the first two factors. Both factors are negative, so their product will be positive.

Step 2 : 

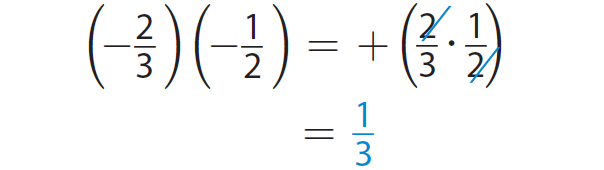
Step 3 :

Now, multiply the result, which is positive, by the third factor, which is negative. The product will be negative.

Step 4 : 

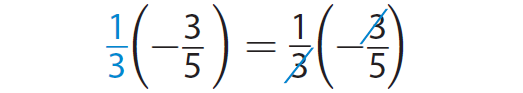
Step 5 :

So,

(-2/3)(-1/2)(-3/5)  =  -1/5

Problem 2 : 

Multiply 1/6, 3/10 and -40. 

Solution : 

Step 1 : 

First, find the product of the first two factors. Both factors are positive, so their product will be positive.

Step 2 : 

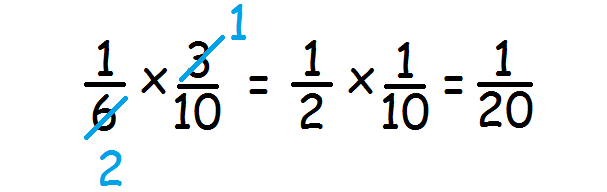
Step 3 :

Now, multiply the result, which is positive, by the third factor, which is negative. The product will be negative.

Step 4 : 

(1/20) x (-40)  =  -40/20  =  -2

Step 5 : 

So,

(1/6) x (3/10) x (-40)  =  -2

Problem 3 : 

Multiply -4, -4.5 and - 2. 

Solution : 

Step 1 : 

First, find the product of the first two factors. Both factors are negative, so their product will be positive.

Step 2 : 

(-4) x (-4.5)  =  18 

Step 3 :

Now, multiply the result, which is positive, by the third factor, which is negative. The product will be negative.

Step 4 : 

(18) x (-2)  =  -36

Step 5 : 

So,

(-4) x (-4.5) x (-2)  =  -36

Problem 4 : 

Multiply -4, -2.5, 5 and - 1.4. 

Solution : 

Step 1 : 

Find the product of the first two factors. Both factors are positive, so their product will be positive.

(-4) x (-2.5)  =  10

Step 2 : 

Now, find the product of the next two factors. Here the factors 5 and -1.4 are having different signs, so their product will be negative.

(5) x (-1.4)  =  7

Step 3 :

Multiply the result in step 1 by the result in step 2. The results in step 1 and step 2 are having the same sign. So their product is positive.     

Step 4 : 

(10) x (7)  =  70

Step 5 : 

So,

(-4) x (-2.5) x (5) x (-1.4)  =  -70

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.