ORDER OF OPERATIONS PRACTICE PROBLEMS WITH ANSWERS

Evaluate each of the following numerical expressions.

Problem 1 :

[3 x (4 + 2)] x 5

Solution :

= [3 x  (4 + 2)] x 5

= [3 x 6] x 5

= 18 x 5 

= 90

Problem 2 :

[4 x (16 – 1)] – 6

Solution :

[4 x (16 – 1)] – 6

= [4 x 15] – 6

= 60 - 6

= 54

Problem 3 :

5 + [6 + (7 x 2)] ÷ 5

Solution :

= 5 + [6 + (7 × 2)] ÷ 5

= 5 + [6 + 14] ÷ 5

= 5 + 20 ÷ 5

= 5 + 4

 = 9

Problem 4 :

3 – (-2 + 7) + 4

Solution :

= 3 – (-2 + 7) + 4

= 3 – 5 + 4

= -2 + 4

= 2

Problem 5 :

(18 ÷ 3) x (-2)

Solution :

= (18 ÷ 3) x (-2)

= 6 x (-2)

= -12

Problem 6 :

2(7 – 13) – (6 - 12)

Solution :

= 2(7 – 13) – (6 - 12)

= 2(-6) – (-6)

= -12 + 6

= -6

Problem 7 :

-6 x (2 – 7)

Solution :

= -6 x (2 – 7)

= -6 x (-5)

= 30

Problem 8 :

–(14 – 8) ÷ (-2)

Solution :

= –(14 – 8) ÷ (-2)

= -6 ÷ (-2)

= 3

Problem 9 :

-18 – (8 – 15)

Solution :

= -18 – (8 – 15)

=-18 – (-7)

= -18 + 7

= -11

So, the answer is -11.

Problem 10 :

-52 ÷ (6 – 19)

Solution :

= -52 ÷ (6 – 19)

= -52 ÷  (-13)

= 4

Problem 11 :

[38 - (-4)]/[6 x (-7)]

Solution : 

= [38 - (-4)]/[6 x (-7)]

= [38 + 4]/[-42]

= 42/[-42]

= -1

Problem 12 :

[38 - (-4)]/[6 x (-7)]

Solution :

= [28 - (-3 x 4)]/[10 x (-2)]

= [28 - (-12)]/[-20]

= [28 + 12]/[-20]

= 40/[-20]

= -2

Problem 13 :

42 ÷ (15 − 2³)

Solution :

= 42 ÷ (15 − 2³)

= 42 ÷ (15 − 8)

= 42 ÷ 7

= 6

Problem 14 :

You need to read 20 poems in 5 days for an English project. Each poem is 2 pages long. Evaluate the expression 20 × 2 ÷ 5 to find how many pages you need to read each day.

Solution :

Evaluating the expression,

= 20 × 2 ÷ 5

From left to right for both multiplciation and division, we will give same importance.

= 40 ÷ 5

= 8

So, number of pages read each day is 8.

Your friend evaluates the expression. Is your friend correct? Explain your reasoning.

Problem 15 :

= 9 + 3 × 3²

= 12 × 9

= 108

Solution :

The above calculation is incorrect, correct steps are

= 9 + 3 × 3²

Use the exponents first,

= 9 + 3 × 9

Perform the multiplication.

= 9 + 27

Add these two terms,

= 36

The answer should be 36.

Problem 16 :

= 19 − 6 + 12

= 19 − 18

= 1

Solution :

The above calculation is incorrect, correct steps are

= 19 − 6 + 12

Adding the numbers,

= 31 - 6

= 25

So, the answer is 25.

Problem 17 :

The diagram shows landing zones for skydivers. Zone 1 is for experts. The remaining space is divided in half and designated as Zones 2 and 3 for tandem divers. What is the area of Zone 2?

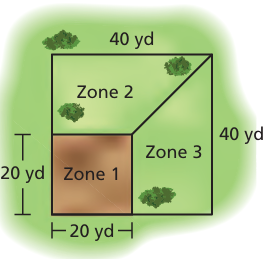
Solution :

Area of zone 2

= (1/2) (area of square whose side length is 40 yards - area of square whose side length is 20 yards)

= (1/2) (40² - 20²)

= (1/2)(1600 - 400)

= (1/2)(1200)

= 600 square yards.

Problem 18 :

A square vegetable garden has side lengths of 12 feet. You plant flowers in the center portion as shown. You divide the remaining space into 4 equal sections and plant tomatoes, onions, zucchini, and peppers. What is the area of the onion section?

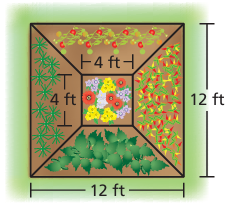
Solution :

Area of onion section

= (1/4) (area of square whose side length is 12 ft - area of square whose side is 4 ft)

= (1/4)(12² - 4²)

= (1/4)(144 - 16)

= (1/4)(128)

= 32 square ft.

So, the required area is 32 square ft.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.