PAIR OF STRAIGHT LINES SOLVED PROBLEMS

Problem 1 :

The slope of one of the straight lines ax² + 2hxy + by² = 0 is twice that of the other, show that 8h² = 9ab.

Solution :

If the given pair of straight line is in the form ax² + 2hxy + by²  =  0, then their exists the following relationship.

m₁ + m₂  =  -2h/b  ------(1)

m₁ m₂  =  a/b  ------(2)

From the question given, we know that 

Slope of one straight line  =  2 (slope of other)

m₁  =  2 m₂

2m₂ + m₂  =  -2h/b

3 m₂  =  -2h/b

m₂  =  -2h/3b

Now we are going to apply m₁  =  2 m₂ and m₂  =  -2h/3b in the second equation.

2 (-2h/3b)(-2h/3b)  =  a/b 

8h²/9b²  =  a/b

8h²  =  9ab

Problem 2 :

The slope of one of the straight lines ax² + 2hxy + by² = 0 is three times the other, show that 3h² = 4ab.

Solution :

If the given pair of straight line is in the form ax² + 2hxy + by²  =  0, then their exists the following relationship.

m₁ + m₂  =  -2h/b  ------(1)

m₁ m₂  =  a/b  ------(2)

From the question given, we know that 

Slope of one straight line  =  3 (slope of other)

m₁  =  3 m₂

3m₂ + m₂  =  -2h/b

4 m₂  =  -2h/b

m₂  =  -2h/4b  =  -h/2b

Now we are going to apply m₁  =  3 m₂ and m₂  =  -h/2b in the second equation.

m₁ m₂  =  a/b

3 m₂m₂  =  a/b

3 (m₂)²  =  a/b

3(-h/2b)²  =  a/b

3h²/4b²  =  a/b

3h²  =  4ab

Problem 3 :

A ΔOPQ is formed by the pair of straight lines x² −4xy +y² = 0 and the line PQ. The equation of PQ is x + y − 2 = 0. Find the equation of the median of the triangle ΔOPQ drawn from the origin O.

Solution :

We cannot find the factors from the pair of straight lines. By solving the given equations, we may get the vertices P and Q.

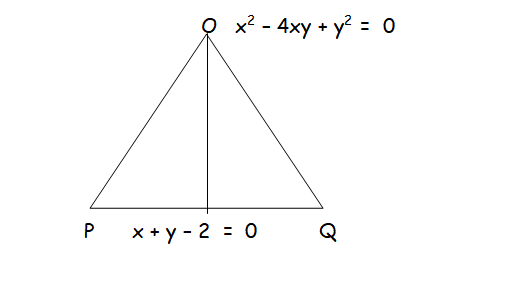
x² −4xy + y² = 0   --------(1)

x + y − 2 = 0   --------(2)

Apply y  =  -x + 2 in the first equation, we get

x² − 4x (-x + 2) + (-x + 2)² = 0

x² + 4x² - 8x + x² - 4x + 4  =  0

6x² - 12x + 4  =  0

3x² - 6x + 2  =  0

x  =  (-b ± √b² - 4ac) / 2a

x  =  [6 ± √6² - 4(3)(2)] / 2(3)

x  =  [6 ± √(36 - 24)] / 2(3)

x  =  [6 ± √12] / 6

x  =  [6 ± 2√3] / 6

x  =  1 ± (√3/3)

Midpoint of PQ :

  =  (x₁ + x₂)/2,  (y₁ + y₂)/2

=  2/2, 2/2

Midpoint of PQ is (1, 1)

Equation of median PQ :

O (0, 0) M (1, 1)

(y - 0)/(1 - 0)  =  (x - 0)/(1 - 0)

y/1  =  x/1

y  =  x

Problem 4 :

Find the equation of lines passing through the point (-1, 2) and perpendicular to the lines x + 2y = 37 and 3x - 4y - 53 = 0

Solution :

Slope of the line x + 2y = 37

2y = -x + 37

y = (-1/2)x + (37/2)

slope = -1/2

Slope of the perpendicular line = 2

Equation of perpendicular line :

(y - y₁) = m(x - x₁)

(y - 2) = 2(x - (-1))

y - 2 = 2x + 2

2x - y + 2 + 2 = 0

2x - y + 4 = 0 -----------(1)

Slope of the line 3x - 4y - 53 = 0

4y = 3x - 53

y = (3/4)x - (53/4)

slope = 3/4

Slope of the perpendicular line = -4/3

Equation of perpendicular line :

(y - y₁) = m(x - x₁)

(y - 2) = (-4/3)(x - (-1))

3(y - 2) = -4(x + 1)

3y - 6 = -4x - 4

4x + 3y - 6 + 4 = 0

4x +  3y - 2 = 0-----------(2)

Equation of pair of lines :

(2x - y + 4)(4x +  3y - 2)

8x² + 6xy - 4x - 4xy - 3y² + 2y + 16x + 12y - 8 = 0

8x² - 3y² + 6xy - 4xy - 4x + 16x + 2y + 12y - 8 = 0

8x² - 3y² + 2xy + 12x + 14y - 8 = 0

8x² + 2xy - 3y² + 12x + 14y - 8 = 0

Problem 5 :

Find the joint equation of a pair of lines through the origin and perpendicular to pair of lines 

2x² - 3xy - 9y² = 0

Solution :

2x² - 3xy - 9y² = 0

2x² - 6xy + 3xy - 9y² = 0

2x(x - 3y) + 3y(x - 3y) = 0

(2x + 3y) (x - 3y) = 0

2x + 3y = 0 and x - 3y = 0

Slope of the perpendicular lines are 3/2 and -3 respectively.

The pair of straight lines passes through the origin.

y = (3/2)x 

2y = 3x

3x - 2y = 0

y = -3x

y + 3x = 0

3x + y = 0

Equation of pair of straight lines which is perpendicular to the given pair of straight lines :

(3x - 2y)(3x + y) = 0

9x² + 3xy - 6xy - 2y² = 0

9x² - 3xy - 2y² = 0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.