PARABOLA AND ELLIPSE WORD PROBLEMS

Problem 1 :

A rod of length 1 2. m moves with its ends always touching the coordinate axes. The locus of a point P on the rod, which is 0 3. m from the end in contact with x -axis is an ellipse. Find the eccentricity.

Solution :

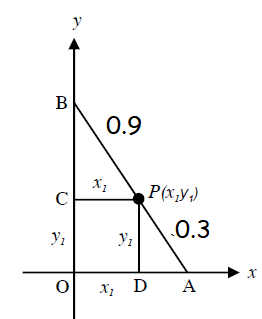
Let AB be the rod and P(x1, y1) be a point on the ladder such that AP = 6m. Draw PD perpendicular to x-axis and

PC perpendicular to y-axis. 

Clearly the triangles ADP and PCB are similar.

PC/DA  =  PB/AP =  BC/PD

x₁/DA  =  0.9/0.3  =  BC/y₁ 

DA = x₁/3, BC  =  3y₁

OA  =  OD + DA  ==> x₁ + (x₁/3)  ==>  4x₁/3

OB  =  OC + BC  ==> y₁ + 3y₁  ==>  4y₁

OA² + OB²  =  AB²

(4x₁/3)² + (4y₁)²  =  (1.2)²

(16/9)x₁² + 16y₁²  =  1.44

16x₁² + 144y₁²  =  1.44(9)

16x₁² + 144y₁²  =  12.96

x₁²/(12.96/16) + y₁²/(12.96/144)  =  12.96/12.96

(x₁²/0.81) + (y₁²/0.09)  =  1

a²  =  81/100, b²  = 9/100

c² = a² - b²

c² = (81 - 9)/100

c² = 72/100

c  =  6√2/10

e = c/a  =   (6√2/10) / (9/10)

e  =  2√2/3

Problem 2 :

Assume that water issuing from the end of a horizontal pipe, 7 5 . m above the ground, describes a parabolic path. The vertex of the parabolic path is at the end of the pipe. At a position 2.5 m below the line of the pipe, the flow of water has curved outward 3 m beyond the vertical line through the end of the pipe. How far beyond this vertical line will the water strike the ground?

Solution :

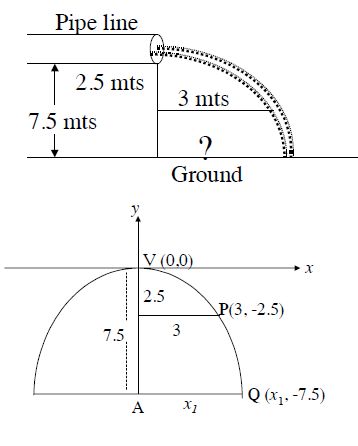
As per the given information, we can take the parabola as open downwards

x² = − 4ay

Let P be the point on the flow path, 2.5m below the line of the pipe and 3 m beyond the vertical line through the end of the pipe.

P is (3, − 2.5)

Thus 9 = − 4a (− 2.5)

a  =  9/10

The equation of the parabola is x² = − 4 × (9/10) y

Let x₁ be the distance between the bottom of the vertical line on the ground from the pipe end and the point on which the water touches the ground. But the height of the pipe from the ground is 7.5 m

The point (x₁, − 7.5) lies on the parabola

x₁² = − 4 × (9/10) × (− 7.5) = 27

x₁ = 3 √3

The water strikes the ground 3 √3 m beyond the vertical line.

Problem 3 :

On lighting a rocket cracker it gets projected in a parabolic path and reaches a maximum height of 4 m when it is 6 m away from the point of projection. Finally it reaches the ground 12 m away from the starting point. Find the angle of projection.

Solution :

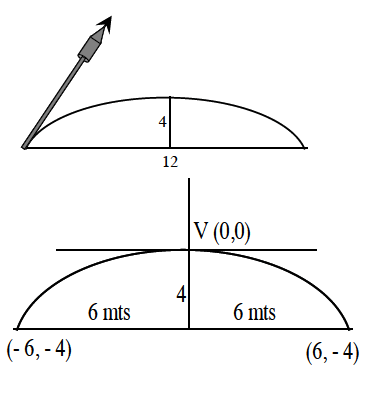
The equation of the parabola is of the form x2 = - 4ay (by taking the vertex at

the origin). It passes through (6, -4)

36 = 16a

a = 9/4

The equation is x² = -9y 

Find the slope at (-6, -4)

Differentiating (1) with respect to x, we get

2x = -9 (dy/dx)

dy/dx = -(2x/9)

Slope at (-6, -4),

(dy/dx) = - (2/9) × - 6 = 4/3

tan θ = 4/3

θ = tan⁻¹ (4/3)

The angle of projection is tan⁻¹ (4/3).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.