PARTIAL FRACTIONS DECOMPOSITION EXAMPLES

Example 1 :

Resolve the following rational expressions into partial fractions.

1/(x²-a²)

Solution :

Let us decompose the denominator into linear factors.

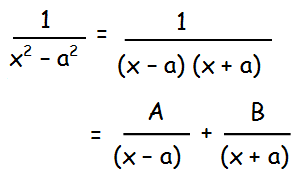
1/(x²-a²)  =  [A(x + a) + B(x - a)]/(x²-a²)

1  =  A(x + a) + B(x - a)

Hence the solution is

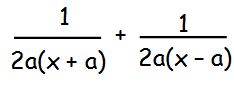
Example 2 :

Resolve the following rational expressions into partial fractions.

(3x + 1)/(x - 2) (x  + 1)

Solution :

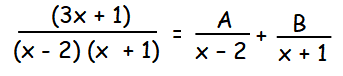
3x + 1  =  A(x + 1) + B(x - 2)

Hence the solution is

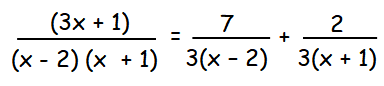
Example 3 :

Resolve the following rational expressions into partial fractions.

x/(x² + 1)(x - 1)(x + 2)

Solution :

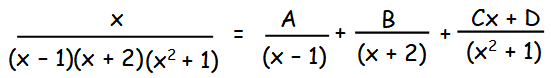
x  = A(x+2)(x²+1) + B(x²+1)(x-1) + (Cx + D)(x-1)(x+2)

When x = 0

x  = A(x+2)(x²+1) + B(x²+1)(x-1) + (Cx + D)(x-1)(x+2)

0  =  A(2)(1) + B(1)(-1) + D(-1)(2)

0  =  2A - B - 2D

By applying the values of A and B, we get

0  =  (1/3) - (2/15) - 2D

2D  =  3/15

D  =  1/10

When x = -1

-1  = A(1)(2) + B(2)(-2) + (-C+D)(-2)(1)

-1  = 2A - 4B + 2C - 2D

By applying the values of A, B and D

-1  = (1/3) - (8/15) + 2C - (1/5)

-1  =  ((5 - 8 - 3)/15) + 2C

-1  =  -6/15 + 2C

-1 + (2/5)  =  2 C  ==> -3/5  =  2C  ==> C  =  -3/10

Hence the solution is

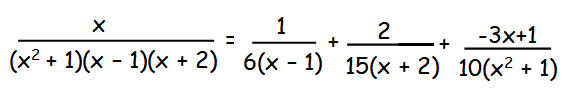
Example 4 :

(-5x + 4)/(x² - x)

Solution :

= (-5x + 4)/(x² - x)

= (-5x + 4)/x(x - 1)

(-5x + 4)/x(x - 1) = A/x + B/(x - 1) ----(1)

-5x + 4 = A(x - 1) + Bx

When x = 1

-5(1) + 4 = B(1)

-5 + 4 = B

B = -1

When x = 0

-5(0) + 4 = A(0 - 1) + B(0)

4 = -A

A = -4

Applying the value of A and B 

(-4/x) - [1/(x - 1)]

Example 5 :

(2x² - 9x - 10)/(x² - 5x)

Solution :

= (2x² - 9x - 10)/(x² - 5x)

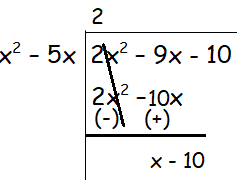
= 2 + [(x - 10)/(x² - 5x)]

= 2 + [(x - 10)/x(x - 5)]

(x - 10)/x(x - 5) = A/x + B/(x - 5)

(x - 10)/x(x - 5) = [A(x - 5) + Bx]/x(x - 5)

x - 10 = A(x - 5) + Bx

When x = 5

5 - 10 = A(5 - 5) + B(5)

-5 = 5B

B = -1

When x = 0

0 - 10 = A(0 - 5) + B(0)

-10 = -5A

A = 10/5

A = 2

Applying the values of A and B, we get

= 2/x + (-1/(x - 5))

Example 6 :

(-2x² + 19x - 13)/(x³ - 7x² + 11x - 5)

Solution :

= (-2x² + 19x - 13)/(x³ - 7x² + 11x - 5)

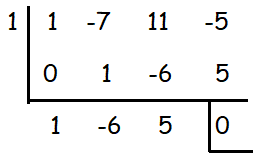
The above synthetic division shows 

= x² - 6x + 5

= (x - 1)(x - 5)

The factors are (x - 1) (x - 1) and (x - 5).

(-2x² + 19x - 13)/(x³ - 7x² + 11x - 5)

= (-2x² + 19x - 13)/(x - 1) (x - 1) (x - 5)

= (-2x² + 19x - 13)/(x - 1)² (x - 5)

= A/(x - 1) + B/(x - 1)² + C/(x - 5)

-2x² + 19x - 13 = A(x - 1)(x - 5) + B(x - 5) + C(x - 1)²

When x = 1

-2(1)² + 19(1) - 13 = A(1 - 1)(1 - 5) + B(1 - 5) + C(1 - 1)²

-2 + 19 - 13 = B(-4)

-15 + 19 = -4B

4B = -4

B  = -1

When x = 5

-2(5)² + 19(5) - 13 = A(5 - 1)(5 - 5) + B(5 - 5) + C(5 - 1)²

-2(25) + 95 - 13 = C(16)

-50 + 95 - 13 = 16C

-63 + 95 = 16C

32 = 16C

C = 32/16

C = 2

When x = 0

-2(0)² + 19(0) - 13 = A(0 - 1)(0 - 5) + B(0 - 5) + C(0 - 1)²

- 13 = 5A - 5B + C(1)

- 13 = 5A - 5(-1) + 2

-13 = 5A + 5 + 2

-13 - 7 = 5A

5A = -20

A = -20/5

A = -4

-4/(x - 1) - 1/(x - 1)² + 2/(x - 5)

Example 7 :

(20x + 9)/(25x² + 20x + 4)

Solution :

= (20x + 9)/(25x² + 20x + 4)

= (20x + 9)/((5x)² + 2(5x)(3) + 2²)

= (20x + 9)/(5x + 2)²

(20x + 9)/(5x + 2)² = A/(5x + 2) + B/(5x + 2)²

(20x + 9) = A(5x + 2) + B

When x = -2/5

20(-2/5) + 9 = 0 + B

B = -8 + 9

B = 1

When x = 0

(20(0) + 9) = A(5(0) + 2) + B

9 = 2A + B

9 = 2A + 1

9 - 1 = 2A

2A = 8

A = 8/2

A = 4

By applying the values of A and B, we get

= 4/(5x + 2) + 1/(5x + 2)²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.