PERIMETER OF RHOMBUS

A rhombus is a four-sided closed figure where the lengths of all the four sides will be equal and also the diagonals will be perpendicular. 

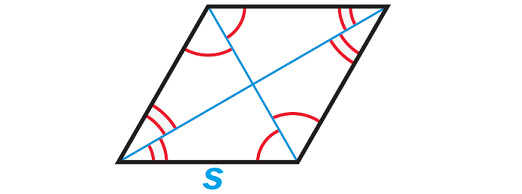
Let 's' be the length of each side of a rhombus.

Perimeter of the Rhombus = 4s

Example 1 :

Find the perimeter of the rhombus whose side length is 16 cm.

Solution :

Formula for perimeter of a rhombus :

=  4s 

Substitute 16 for s.

=  4(16)

=  64

So, the perimeter of the rhombus is 64 cm.

Example 2 :

If the perimeter of a rhombus is 72 inches, then find the length of each side. 

Solution :

Perimeter of the rhombus  =  72 inches

4s  =  72

Divide each side by 4.

 s  =  16 

So, the length of each side of the rhombus is 16 inches. 

Example 3 :

A rhombus has side length of 500 cm. Find its perimeter in meter.

Solution :

Formula for perimeter of a rhombus :

=  4s 

Substitute 500 for s.

=  4(500)

=  2000 cm -----(1)

We know  

100 cm  =  1 m

Therefore, to convert centimeter to meter,  we have to divide by 100. 

(1)-----> Perimeter  =  2000 cm

Divide the right side by 100 to convert cm into m.

Perimeter  =  (2000 / 100) m

=  20 m

So, perimeter of the rhombus is 20 meters.

Example 4 :

If the length of each side of a rhombus is (3x + 4) and its perimeter is 76 units, find the value of x. 

Solution :

Perimeter of the rhombus  =  76 units

4s  =  76

Divide each side by 4.

s  =  19

Substitute (3x + 4) for s. 

3x + 4  =  19

Subtract 4 from each side. 

3x  =  15

Divide each side by 3. 

x  =  5

Example 5 :

In the diagram shown below, if PQRS is a rhombus, then find its perimeter. 

Solution :

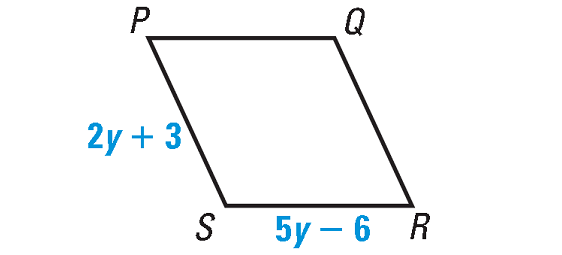
All four sides of a rhombus are congruent. 

So, 

RS  =  PS

5y - 6  =  2y + 3

Subtract 2y from each side.

3y - 6  =  3

Add 6 to each side. 

3y  =  9

Divide each side by 3. 

y  =  3

To find the length of each side of the rhombus, substitute 3 for y either in '2y + 3' or '5y - 6'.

2y + 6  =  2(3) + 3

2y + 6  =  6 + 3

2y + 6  =  9

So, the length of each side of the rhombus is 9 units. 

Formula for perimeter of a rhombus :

=  4s 

Substitute 9 for s.

=  4(9)

=  36

So, perimeter of the rhombus is 36 units. 

Example 6 :

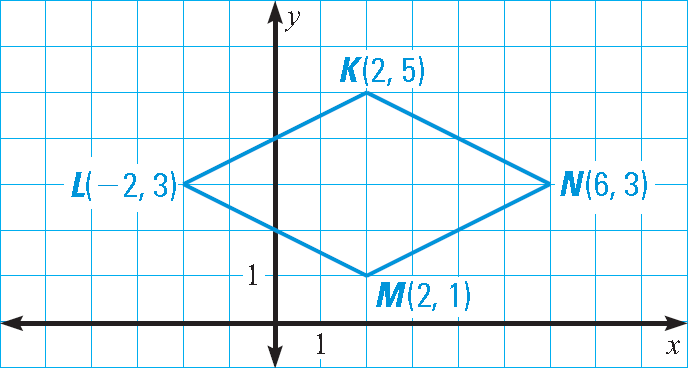
Find the perimeter of the rhombus shown below. 

Solution :

Find the length of the side MN in the above rhombus using distance formula. 

MN  =  √[(x₂ - x₁)² + (y₂ - y₁)²]

Substitute (x₁, y₁)  =  (2, 1) and (x₂, y₂)  =  (6, 3).  

LM  =  √[(x₂ - x₁)² + (y₂ - y₁)²]

LM  =  √[(6 - 2)² + (3 - 1)²]

LM  =  √(4² + 2²)

LM  =  √(16 + 4)

LM  =  √20

LM  =  2√5

All four sides of a rhombus are congruent. 

Then, the length of each side of the above rhombus is 2√5 units. 

Formula for perimeter of a rhombus :

=  4s 

Substitute 2√5 for s.

=  4(2√5)

=  8√5

So, perimeter of the rhombus is 8√5 units. 

Example 7 :

In the rhombus ABCD shown below, if the lengths of the diagonals AC and BD are 10 units and 8 units respectively, find its perimeter. 

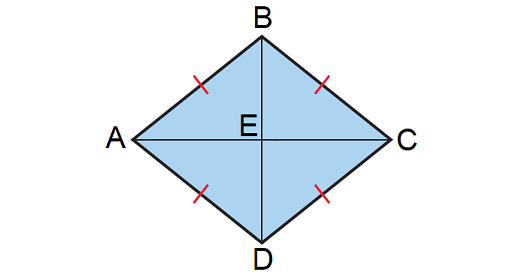
Solution :

The diagonals of a rhombus will be perpendicular and they will bisect each other. 

Then, we have

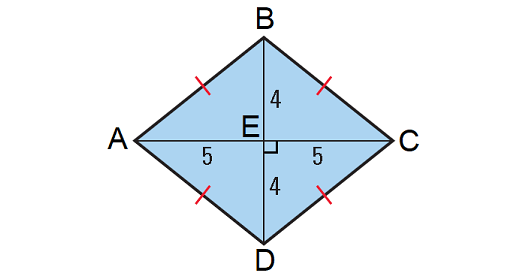
In the above rhombus, consider the right angled triangle CDE. 

By Pythagorean Theorem, 

CD²  =  DE² + CE²

CD²  =  4² + 5²

CD²  =  16 + 25

CD²  =  41

CD  =  √41

All four sides of a rhombus are congruent. 

Then, the length of each side of the above rhombus is √41 units. 

Formula for perimeter of a rhombus :

=  4s 

Substitute √41 for s.

=  4√41

So, perimeter of the rhombus is √41 units. 

Example 8 :

The length of the diagonals of a rhombus are 24 cm and 10 cm, respectively. Find out the length of all its sides.

Solution :

In rhombus all sides will be equal. Let x be the length of side. Diagonals will bisect each other at right angle.

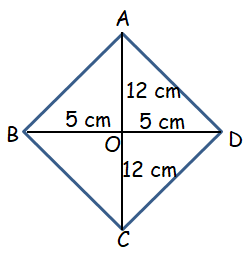
AD² = AO² + OD²

AD² = 12² + 5²

AD² = 144 + 25

AD² = 169

AD = 13 cm

Perimeter of rhombus = 4(13)

= 52 cm

Example 9 :

Find the length of a side of a rhombus whose perimeter is 60 cm .

Solution :

Perimeter of rhombus = 60 cm 

Side length of rhombus be x

4x = 60

x = 60/4

x = 15

So, side length of rhombus is 15 cm.

Example 10 :

If each side of a rhombus is doubled, how much will its area increase?

(a) 1.5 times    (b) 2 times    (c) 3 times   (d) 4 times

Solution :

Let x be the side of the rhombus and h be the height.

Area = xh

Since the side is doubled, 2x will be the new side.

Area = 2x h

So, option b is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.