PERMUTATION AND COMBINATION
PROBLEMS

Problem 1 :

A committee of 7 members is to be chosen from 6 artists, 4 singers and 5 writers. In how many ways can this be done if in the committee there must be at least one member from each group and at least 3 artists ?

Solution :

For the given condition, possible ways to select members for a committee of 7 members.

(3A, 3S, 1W) ----> 6C3 ⋅ 4C3 ⋅ 5C1  =  20 ⋅ 4 ⋅ 5 = 400

(3A, 1S, 3W) ----> 6C3 ⋅ 4C1 ⋅ 3C1  =  20 ⋅ 4 ⋅ 10 = 800

(3A, 2S, 2W) ----> 6C3 ⋅ 4C2 ⋅ 5C2 = 20 ⋅ 6 ⋅ 10 = 1200

(4A, 2S, 1W) ----> 6C4 ⋅ 4C2 ⋅ 5C1 = 15 ⋅ 6 ⋅ 5 = 450

(4A, 1S, 2W) ----> 6C4 ⋅ 4C1 ⋅ 5C2 = 15 ⋅ 4 ⋅ 10 = 600

(5A, 1S, 1W) ----> 6C5 ⋅ 4C1 ⋅ 5C1 = 6 ⋅ 4 ⋅ 5 = 120

Thus, the total no. of ways is

= 400 + 800 + 1200 + 450 + 600 + 120

= 3570

Problem 2 :

The supreme court has given a 6 to 3 decisions upholding a lower court. Find the number of ways it can give a majority decision reversing the lower court.

Solution :

Upholding a lower court means, supporting it for its decision.

Reversing a lower court means, opposing it for its decision.

In total of 9 cases (6 + 3 = 9), it may give 5 or 6 or 7 or 8 or 9 decisions reversing the lower court. And it can not be 4 or less than 4. Because majority of 9 is 5 or more.

The possible combinations in which it can give a majority decision reversing the lower court are

5 out of 9 ----> 9C5 = 126

6 out of 9 ----> 9C6 = 84

7 out of 9 ----> 9C7 = 36

8 out of 9 ----> 9C8 = 9

9 out of 9 ----> 9C9 = 1

Thus, the total number of ways is

= 126 + 84 + 36 + 9 + 1

= 256

Problem 3 :

Five bulbs of which three are defective are to be tried in two bulb points in a dark room. Find the number of trials in which the room can be lighted.

Solution :

Given : 3 bulbs are defective out of 5.There are two bulb points in the dark room.

One bulb (or two bulbs) in good condition is enough to light the room.

Since there are two bulb points, we have to select 2 out of 5 bulbs.

No. of ways of selecting 2 bulbs out of 5 is

= 5P2

= 10

(It includes selecting two good bulbs, two defective bulbs, one good bulb and one defective bulb. So, in these 10 ways, room may be lighted or may not be lighted)

Number of ways of selecting 2 defective bulbs out of 3 is

= 3C2

= 3

(It includes selecting only two defective bulbs. So, in these 3 ways, room can not be lighted)

The number of ways in which the room can be lighted is

= 10 - 3

= 7

Problem 4 :

Find the number of ways of selecting 4 letters from the word EXAMINATION.

Solution :

There are 11 letters in the word of which A,I,N are repeated twice.

Thus, we have 11 letters of 8 different kinds as given below.

(A, A), (I, I), (N, N), E, X, M, T, O

The group of 4 letters can be selected in any one of the following 4 forms.

(i) 2 alike and other 2 alike.

(ii) 2 alike and other 2 different.

(iii) All 4 different.

Case (i) :

If 2 are alike and other 2 are also alike, any 2 of the 3 groups

(A, A),(I, I),(N, N)

will be selected.

The number of ways is

= 3C2

= 3

Case (ii) :

If 2 are alike and other 2 are different, any one of the three groups

(A, A), (I, I), (N, N)

and 2 letters from 7 different letters are selected.

[E, X, M, T, O + 2 different letters from (A, A), (I, I),(N, N), because one of the groups is already selected]

The number of ways is

= 3C1 ⋅ 7C2

= 3 ⋅ 21

= 63

Case (iii) :

If all four are different, 4 from 8 different letters

A, I, N, E, X, M, T, O

are selected.

The number of ways  is

= 8C4

= 70

Thus the total number of ways is

= 3 + 63 + 70

= 136

Problem 5 :

The letters of the word ZENITH are written in all possible orders. If all the words are written in a dictionary, what is the rank or order of the word ZENITH ?

Solution :

Number of new words formed with the letters of the word.

ZENITH  =  6!  =  720

Alphabetical order of the letters of the word ZENITH is

E, H, I, N, T, Z

Dictionary gives meanings in the order starting with E,H and so on.

Number of words can be formed starting with E,H and so on.

E  __  __  __  __  __  =  5! = 120 words

H  __  __  __  __  __  =  5! = 120 words

I  __  __  __  __  __  =  5! = 120 words

N  __  __  __  __  __  =  5! = 120 words

T  __  __  __  __  __  =  5! = 120 words

Z  E  H  __  __  __  =  3! = 6 words

Z E I  __  __  __  =  3! = 6 words

Z E N H  __  __  =  2! = 2 words

Z E N I H  __  =  1! = 1 word

Z E N I T H  =  1! = 1 word

Thus, the total number of words is

=  120 + 120 + 120 + 120 + 120 + 6 + 6 + 2 + 1 + 1

=  616

Hence, the rank or order of the word ZENITH is 616.

Problem 6 :

A committee of parents is made up of 20 delegates of which 10 represent the primary school, 6 the intermediate school and 4 the secondary school. A committee of 6 people is to be formed.

a. How many different committees are there?

b. How many different committees are there if only the primary school is represented?

Solution :

Part (a) :

Total number of delegates given = 20.

We have to select 6 people of these 20 delegates to form a committee.

20C6 = 38760

Hence, 38760 different committees are three.

Part (b) :

Number of delegates from primary school = 10.

We have to select 6 people of these 10 delegates to form a committee.

10C6 = 10C4

= 210

Hence, 210 different committees are three if only the primary school is represented.

Problem 7 :

A hospital decides to send a delegation of 8 doctors to a conference. These 8 doctors are chosen chosen from a group of 17 among which there are 6 surgeons. How many ways are there if at least 4 surgeons must be in the delegation?

Solution :

We need to select 8 doctors out of a group 17 doctors. In the selected 8 doctors, there must at least 4 surgeons.

So, we have to select minimum 4 surgeons.

The possible options are :

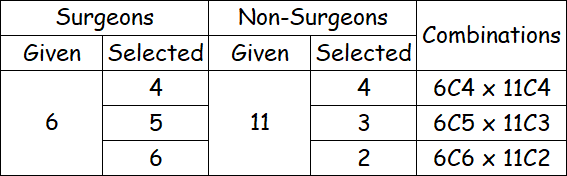
There are six possible options to select 8 doctors.

6C4 x 11C4 = 15 x 330 = 4950

6C5 x 11C3 = 6 x 165 = 990

6C6 x 11C2 = 1 x 55 = 55

We can not apply all the above options simultaneously. We can apply only one of them at a time, the first option or second option or third option.

According to the fundamental principles of counting, we have to use 'addition rule'.

OR ----> Addition

Therefore, the number of ways to select 8 doctors in which there are at least 4 surgeons :

= 1^st option or 2^nd option or 3^rd option

= 1^st option + 2^nd option + 3^rd option

= 4950 + 990 + 55

= 5995

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.