PLOT THE COMPLEX NUMBER IN THE COMPLEX PLANE

Plot all four points in the same complex plane.

Example 1 :

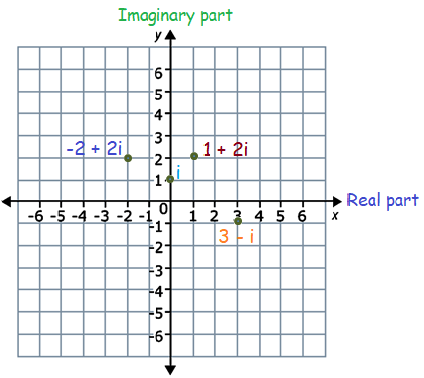
1 + 2i, 3 - i, -2 + 2i, i

Solution :

Given, complex numbers are 1 + 2i, 3 - i, -2 + 2i, i

We are taking the real part of the complex number on the x-coordinate and the imaginary part on the y-coordinate.

Then, the ordered pair of the complex numbers are

So, the four points are (1, 2), (3, -1), (-2, 2) and (0, 1).

By plotting the four points on the complex plane, we get

Example 2 :

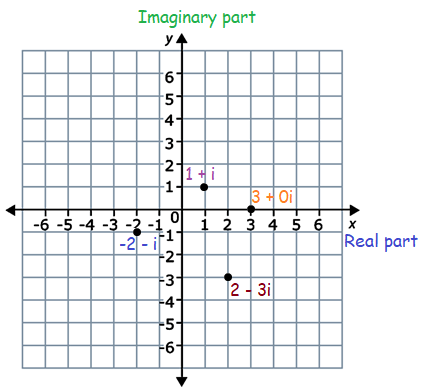
2 - 3i, 1 + i, 3, -2 - i

Solution :

Given, complex numbers are 2 - 3i, 1 + i, 3, -2 - i

Then, the ordered pair of the complex numbers are

So, the four points are (2, -3), (1, 1), (3, 0) and (-2, -1).

By plotting the four points on the complex plane, we get

Example 3 :

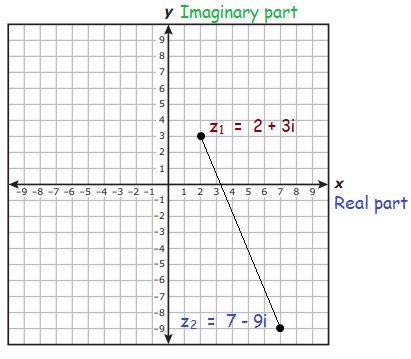
Find the distance between two complex numbers z₁  =  2 + 3i and z₂  =  7 - 9i on the complex plane.

Solution :

Given, z₁  =  2 + 3i and z₂  =  7 - 9i are complex numbers.

Then, the ordered pair of the complex numbers are

z₁  =  (2, 3) and z₂  =  (7, -9)

Now, we have the two points (2, 3) and (7, -9)

By plotting the two points on the complex plane, we get

Finding the distance  :

Formula for distance,

d  =  √[(x₂ - x₁)² + (y₂ - y₁)²]

(2, 3)----->(x₁, y₁)

(7, -9)----->(x₂, y₂)

d  =  √[(7 - 2)² + (-9 - 3)²]

d  =  √[(5)² + (-12)²]

d  =  √(25 + 144)

d  =  √169

d  =  13 units

So, the distance is 13 units.

Example 4 :

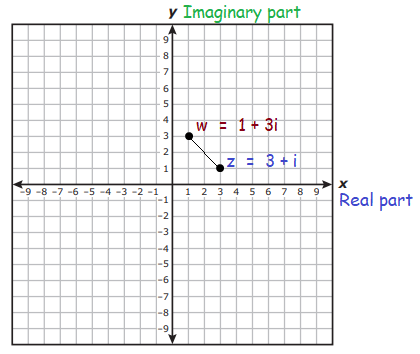
Find the distance and midpoint between two complex numbers z  =  3 + i and w  =  1 + 3i on the complex plane.

Solution :

Given, z  =  3 + i and w  =  1 + 3i are complex numbers.

Then, the ordered pair of the complex numbers are

z  =  (3, 1) and w  =  (1, 3)

Now, we have the two points (3, 1) and (1, 3)

By plotting the two points on the complex plane, we get

Finding the distance :

Formula for distance,

d  =  √[(x₂ - x₁)² + (y₂ - y₁)²]

(3, 1)----->(x₁, y₁)

(1, 3)----->(x₂, y₂)

d  =  √[(1 - 3)² + (3 - 1)²]

d  =  √[(-2)² + (2)²]

d  =  √(4 + 4)

d  =  √8

d  =  2√2 units

So, the distance is 2√2 units.

Finding the midpoint :

Formula for midpoint,

M  =  [(x₁ + x₂)/2, (y₁ + y₂)/2]

=  [(3 + 1)/2, (1 + 3)/2]

Midpoint  =  (2, 2)

So, the midpoint is (2, 2)

Example 5 :

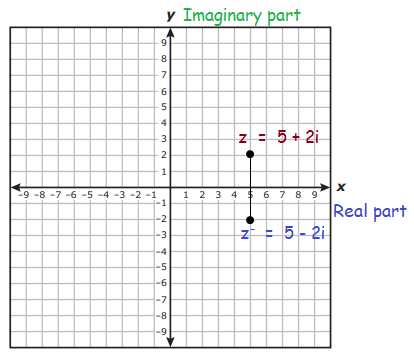
Find the distance and midpoint between the complex number z  =  5 + 2i and its conjugate z^-  =  5 - 2i on the complex plane.

Solution :

Given, z  =  5 + 2i and z^-  =  5 - 2i are complex numbers.

Then, the ordered pair of the complex numbers are

z  =  (5, 2) and z^-  =  (5, -2)

Now, we have the two points (5, 2) and (5, -2)

By plotting the two points on the complex plane, we get

Finding the distance :

Formula for distance,

d  =  √[(x₂ - x₁)² + (y₂ - y₁)²]

(5, 2)----->(x₁, y₁)

(5, -2)----->(x₂, y₂)

d  =  √[(5 - 5)² + (-2 - 2)²]

d  =  √[(-4)²]

d  =  √16

d  =  4 units

So, the distance is 4 units.

Finding the midpoint :

Formula for midpoint,

M  =  [(x₁ + x₂)/2, (y₁ + y₂)/2]

=  [(5 + 5)/2, (2 - 2)/2]

Midpoint  =  (5, 0)

So, the midpoint is (5, 0)

Related pages

• Dividing complex numbers
• Multiplication of complex numbers

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.