POINT LINE AND PLANE POSTULATES WORKSHEET

Problem 1 :

Use the diagram shown below to give examples of point line and plane postulates. 

Problem 2 : 

(i) Rewrite the following postulate in 'if-then' form.  

"A plane contains at least three noncollinear points"

(ii) Write the inverse, converse and contrapositive of the above postulate. 

Problem 3 : 

Decide whether the statement is true or false. If it is false, give a counter example. 

(i) A line can be in more than one plane. 

(ii) Four noncollinear points are always coplanar. 

(iii) Two intersecting lines can be noncoplanar. 

Detailed Answer Key

Problem 1 :

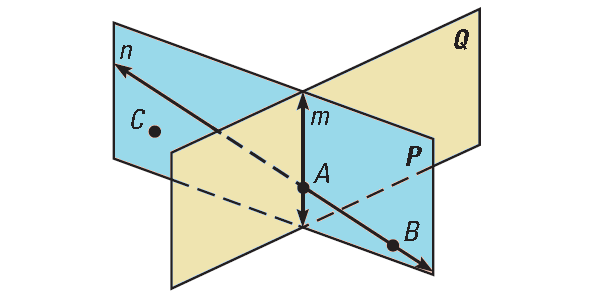
Use the diagram shown below to give examples of point line and plane postulates. 

Solution : 

Postulate 1 : 

There is exactly one line (line n) that passes through the points A and B. 

Postulate 2 : 

Line n contains at least two points. For instance, line n contains the points A and B. 

Postulate 3 : 

Lines m and n intersect at point A. 

Postulate 4 : 

Plane P passes through the noncollinear points A, B and C. 

Postulate 5 : 

Plane P contains at least three noncollinear points A, B and C. 

Postulate 6 : 

Points A and B lie in plane P. So, line n, which contains points A and B, also lies in plane B.    

Postulate 7 : 

Planes P and Q intersect. So, they intersect in a line, labeled in the diagram as line m.    

Problem 2 : 

(i) Rewrite the following postulate in 'if-then' form.  

"A plane contains at least three noncollinear points"

(ii) Write the inverse, converse and contrapositive of the above postulate. 

Solution (i) :

"A plane contains at least three noncollinear points"

The above postulate can be written in 'if-then' form as follows :

If two points are distinct, then there is exactly one line that passes through them.  

Solution (ii) :

"A plane contains at least three noncollinear points"

Inverse :

If two points are not distinct, then  it is not true that there is exactly one line that passes through them.  

Converse :

If exactly one line passes through two points, then the two points are distinct. 

Contrapositive :

If it is not true that exactly one line passes through two points, then the two points are not distinct. 

Problem 3 : 

Decide whether the statement is true or false. If it is false, give a counter example. 

(i) A line can be in more than one plane. 

(ii) Four noncollinear points are always coplanar. 

(iii) Two intersecting lines can be noncoplanar. 

Solution (i) : 

In the diagran shown below, line k is in plane S and line k is in plane T.  

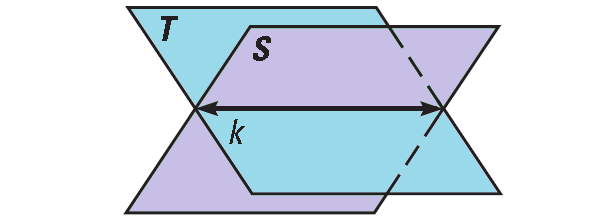
So, it is true that a line can be in more than one plane. 

Solution (ii) : 

Consider the points A, B, C and D shown below. The points A, B and C lie in a plane, but there is no plane that contains all four points. 

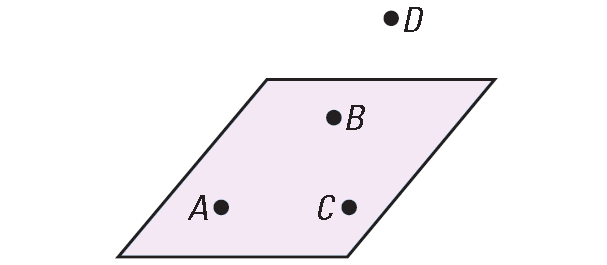
So, as shown in the counter-example above, it is false that four noncollinear points are always coplanar. 

Solution (iii) : 

In the diagram shown below, line m and line n are non intersecting and are also noncoplanar. 

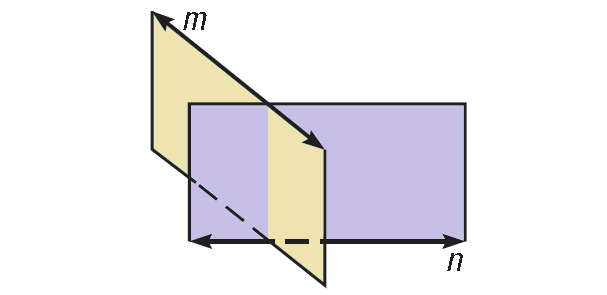
So, it is true that two nonintersecting lines can be noncoplanar. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.