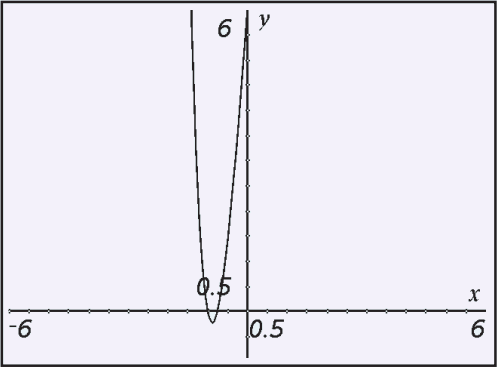
HOW TO FIND THE ROOTS OF A POLYNOMIAL OF DEGREE 4

Example 1 :

Solve the equation

x⁴+4x³+5x²+2x-2  =  0

which one root is -1 + i

Solution :

Let 

f(x)  =  x⁴ + 4x³ + 5x² + 2x - 2

Since one of the root is complex number, the other root may be its conjugate.

So,  α = -1 + i  β = - 1 - i

By using these two roots we can find a quadratic equation which is the part of the original equation. First, let us find the quadratic equation.

General form of any quadratic equation:

 x²-(α+β)x+αβ = 0

α  =  -1+i  β  =  -1-i

Sum of roots (α+β)  =  -1+i-1-i

= - 2

Product of roots (αβ)  =  (-1+i) (-1-i)

=  (-1)² - i²

=  2

Therefore the required quadratic equation 

x²-(-2)x+2  =  0

x²+2x+2  =  0

This is the part of the equation of polynomial of degree 4.

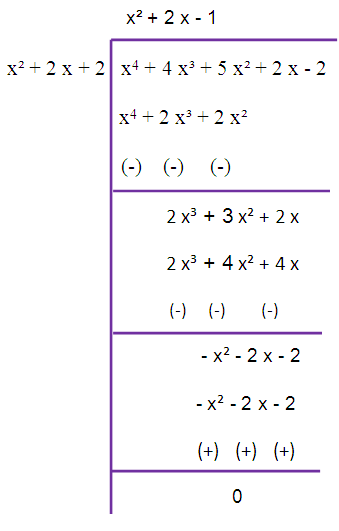
By solving this quadratic equation

x²+2x-1  =  0

we get other two roots.

a = 1, b = 2, c = -1

x  =  [- b ± √(b²-4 a c)]/2 a

x  =  [-2 ± √(2²-4 (1)(-1))]/2 (1)

x  =  [- 2 ± √8]/2

x  =  [- 2 ± 2 √2]/2

x  =  -1±√2

Therefore the four roots are

-1 + i ,- 1 - i , - 1 + √2 , - 1 - √2.

Example 2 :

Solve the equation

6x⁴ − 35x³ + 62x² − 35x + 6 = 0

Solution :

By suing synthetic division repeatedly, we may solve this problem.

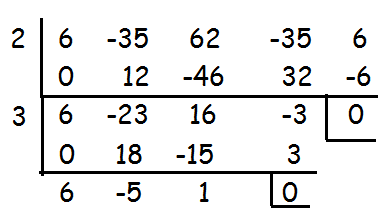
2 and 3 are the solutions of the given polynomial. To know the other solutions, let us solve the quadratic equation.

6x² - 5x + 1  =  0

6x² - 2x - 3x + 1  =  0

2x (3x - 1) - 1(3x - 1)  =  0

(2x - 1) (3x - 1)  =  0

2x - 1  =  0 and 3x - 1  =  0

x  =  1/2  and x  =  1/3

Hence the solutions are 2, 3, 1/2 and 1/3

Example 3 :

Solve

x⁴ + 3x³ - 3x - 1  =  0

Solution :

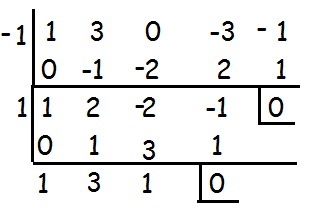
1 and -1 are the solutions of the given polynomial, to find other two solutions, let us solve the quadratic equation

x² + 3x + 1  =  0

x = -b ± √(b² - 4ac) / 2a

x = -3 ± √(9 - 4) / 2(1)

x = (-3 ± √5)/2

So, roots are -1, 1, (-3 ± √5)/2.

Example 4 :

Solve the equation 6x⁴ − 5x³ − 38x² − 5x + 6 = 0 if it is known that 1/3 is a solution.

Solution :

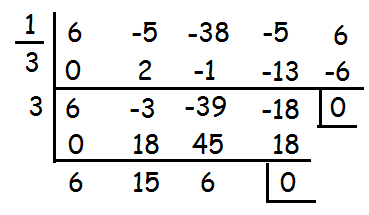
1/3 and 3 are solutions of the given polynomial, to find other two solutions, let us solve the quadratic equation.

6x² + 15x + 6  =  0

6x² + 12x + 3x + 6  =  0

6x(x + 2) + 3(x + 2)  =  0

(6x + 3)(x + 2)  =  0

x  =  -1/2 and x = -2

Hence the solutions are -1/2, -2, 3 and 1/3.

Example 5 :

Solve the equation x⁴ −14x² + 45 = 0

Solution :

Let x²  =  t

t² − 14t + 45 = 0

t² − 9t - 5t + 45 = 0

t(t - 9) - 5(t - 9)  =  0

(t - 5) (t - 9)  =  0

t  =  5 and t  =  9

x²  =  5, x²  =  9

x  =  ±√5, x = ±3

Hence the solutions are √5, -√5, 3 and -3.

I can find the roots of a given polynomial using factoring. Factor each polynomial and state the roots.

Example 6 :

x⁴ - 3x³ - 4x² = 0

Solution :

x⁴ - 3x³ - 4x² = 0

x² (x² - 3x - 4 ) = 0

x² (x - 4)(x + 1) = 0

x² = 0, x - 4 = 0 and x + 1 = 0

x = 0, x = 4 and x = -1

So, the roots are -1, 0 and 4.

Example 7 :

x³ + 3x² - x - 3 = 0

Solution :

x³ + 3x² - x - 3 = 0

x² (x + 3) - 1 (x + 3) = 0

(x²  - 1)(x + 3)= 0

x² - 1 = 0, x + 3 = 0

x² = 1, x = -3

x = √1 and x = -3

x = ± 1 and x = -3

So, the roots are -1, -3, 1.

Example 8 :

x⁴ + 5x³ - x² - 5x = 0

Solution :

x⁴ + 5x³ - x² - 5x = 0

Factoring x, we get

x(x³ + 5x² - x - 5) = 0

Using grouping method, we get

x[x² (x + 5) - 1(x + 5)] = 0

x(x² - 1)(x + 5) = 0

Equating each factor to 0, we get

So, the solutions are -5, -1, 0 and 1.

Example 9 :

x⁴ - 10x² + 9 = 0

Solution :

Let x² = t

(x²)² - 10x² + 9 = 0

t² - 10t + 9 = 0

(t - 9)(t - 1) = 0

Equating each factor to 0, we get

t = 9 and t = 1

Applying the value of t, we get

x² = 9 and x² = 1

x = ±3 and x = ±1

x = -3, -1, 1 and 3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.