PRACTICAL PROBLEMS ON RELATIONS AND FUNCTIONS IN SET THEORY

Problem 1 :

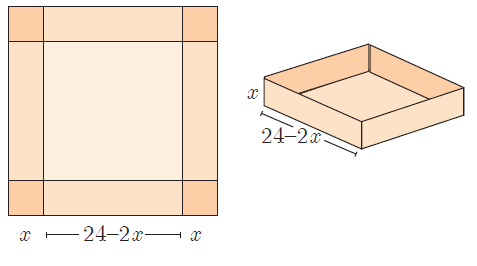
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal squares from the corners and turning up the sides as shown. Express the volume V of the box as a function of x.

Solution :

Since the original shape is square, length of all sides will be equal.

length  =  width  =  24 - 2x 

height  =  x

Volume of cuboid  =  length ⋅ width ⋅ height

  =  (24 - 2x) ⋅ (24 - 2x) ⋅ x

=  x(24 - 2x)²

=  x [24² - 2(24) (2x) + (2x)²]

=  x [576 - 96x + 4x²]

V (x)  =  4x³ - 96x² + 576x

Hence the volume of the cuboid is 4x³ - 96x² + 576x.

Problem 2 :

A function f is defined by f (x) = 3−2x . Find x such that f (x²) = (f (x))² .

Solution :

Given that :

f (x)  =  3 − 2x 

f (x²)  =  3 − 2x² ------(1)

 (f (x))²  =  (3 − 2x)²

=  3² - 2(3)(2x) + (2x)²

 (f (x))²  =  9 - 12x + 4x²  ----(2)

(1)  =  (2)

3 − 2x²  =  9 - 12x + 4x² 

4x² + 2x² - 12x + 9 - 3  =  0

6x² - 12x + 6  =  0

x² - 2x + 1  =  0

(x - 1)²  =  0

x - 1  =  0 (or)  x - 1  =  0

x  =  1 (or) x  =  1

Problem 3 :

A plane is flying at a speed of 500 km per hour. Express the distance d travelled by the plane as function of time t in hours.

Solution :

Time  =  Distance / speed

Speed of plane  =  500 km per hour

Distance travelled  =  d

time taken  =  t in hours

t  =  d/500

d  =  500t

Hence the required distance is 500 t.

Problem 4 :

The data in the adjacent table depicts the length of a woman’s forehand and her corresponding height. Based on this data, a student finds a relationship between the height (y) and the forehand length(x) as y = ax +b , where a, b are constants.

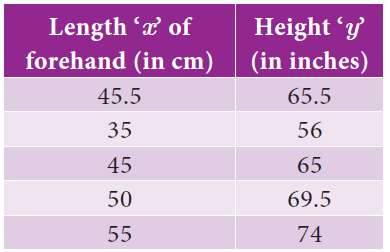
(i) Check if this relation is a function.

(ii) Find a and b.

(iii) Find the height of a woman whose forehand length is 40 cm.

(iv) Find the length of forehand of a woman if her height is 53.3 inches.

Solution :

y = ax + b 

(i)  For every values of x, we get different values of y.Hence it is a function.

(ii)

By solving these two equation, we get a and b

(1) - (2)

(45.5 a + b) - (35a + b)  =  65.5 - 56

45.5 a - 35a + b - b  =  9.5

10.5a  =  9.5

a  =  9.5/10.5

a  =  0.90

Substitute a = 0.90 in (1),

45.5(0.90) + b  =  65.5

b  =  65.5 - 40.95

b  =  24.5

y = 0.9x + 24.5

(iii) Find the height of a woman whose forehand length is 40 cm.

y = ? if x = 40

y = 0.9(40) + 24.5

y = 60.5 

Height of woman is 60.5 inches.

(iv)  x = ? if y = 53.3

53.3 = 0.9x + 24.5

53.3 - 24.5  =  0.9x 

28.8/0.9  =  x

x  =  32

Length of forehand is 32 inches.

Problem 5 :

If R(x) = (2x - 3) / (x + 2)

a)  Evaluate i) R(0)    ii)  R(1)  iii) R(-1/2)

b)  Find the value of x, where R(x) does not exists.

c)  Find R(x - 2) in simplest form.

d)  Find x, if R(x) = -5

Solution :

Given that,  R(x) = (2x - 3) / (x + 2)

i) R(0)

If x = 0

R(0) = (0 - 3) / (0 + 2) ==> -3/2

ii)  R(1)

If x = 1

R(1) = (2 - 3) / (1 + 2) ==> -1/3

iii) R(-1/2)

If x = -1/2

R(-1/2) = (-1 - 3) / ((-1/2) + 2) ==> -4 / (3/2)

= -8/3

b)  R(x) will become does not exists, when the denominator becomes 0

When x = -2, x + 2 will become 0.

c)  To find R(x - 2), we have to apply x as x - 2 in the given function.

R(x) = (2(x - 2) - 3) / (x - 2 + 2)

= (2x - 4 - 3) / x

= (2x - 6) / x

d)  Find x, if R(x) = -5

When R(x) = -5

-5 = (2x - 3) / (x + 2)

-5(x + 2) = 2x - 3

-5x - 10 = 2x - 3

-5x - 2x = -3 + 10

-7x = 7

x = -1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.