PRACTICE PROBLEMS OF FINDING INVERSE FUNCTIONS

For each of the following functions :

Problem 1 :

a) f(x)  =  2x+5         Solution

b) f(x)  =  (3-2x)/4        Solution

c) f(x)  =  x+3        Solution

(i) Find f^-1(x)        Solution

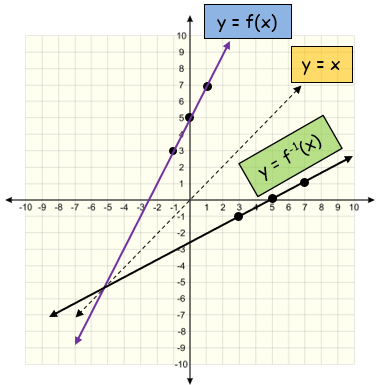
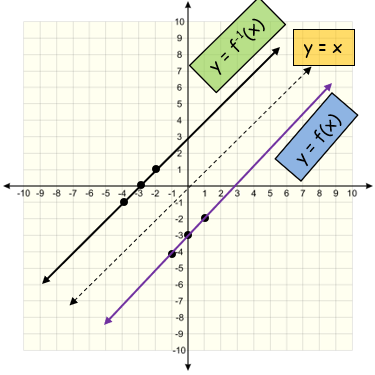
(ii) sketch y  =  f(x), y  =  f^-1(x) and y  =  x on the same axes.        Solution

Problem 2 :

If f(x)  =  2x + 7, find :

a) f^-1(x)        b) f(f^-1(x))        c) f^-1(f(x))

Solution

Problem 3 :

If f(x)  =  (2x + 1)/(x + 3), find :

a) f^-1(x)     b) f(f^-1(x))     c) f^-1(f(x))

Solution

Problem 4 :

You need a total of 50 pounds of two types of ground beef costing $1.25 and $1.60 per pound, respectively. A model for the total cost of the two types of beef is

y = 1.25x + 1.60(50 - x)

where is the number of pounds of the less expensive ground beef.

(a) Find the inverse function of the cost function. What does each variable represent in the inverse function?

(b) Determine the number of pounds of the less expensive ground beef purchased when the total cost is $73.

Solution

Problem 5 :

The function given by

f(x) = k(2 - x - x²)

has an inverse function f^-1(3) = -2, find k.

Solution

(1) 

(a)  (i)  f^-1(x)  =  (x-5)/2

(ii)  

b)  (i)  f^-1(x)  =  -2x+(3/2)

(ii)

c) (i)  f^-1(x)  =  x-3

(ii) 

(2)  (a)  f^-1(x)  =  (x-7)/2

b)  f(f^-1(x))  =  x

c) f^-1(f(x))  =  x

(3)

(a)  f^-1(x)  =  (1-3x)/(x-2)

b)  f(f^-1(x))  =  x  ------(1)

c)  f^-1(f(x))  =  x  ------(2)

4) a) f^-1(x) = (80 - x)/0.35

b)  So, 20 pounds is the answer.

5)  So, the required value of k is -3/4.

(4)  f^-1(x)  =  (x - 3) / 2

(5)  h^-1(x)  =  10^x

Example 1 :

Find the inverse of the function f(x) = x - 5.

Solution

Example 2 :

Find the inverse of the function f(x) = 3x + 5.

Solution

Example 3 :

Find the inverse of the function f(x) = x².

Solution

Example 4 :

Find the inverse of the function f(x) = log₅(x).

Solution

Example 5 :

Find the inverse of the function f(x) = log₅(x). 

Solution

Example 6 :

Find the inverse of the function f(x) = √(x + 1).

Solution

Example 7 :

Consider the function f(x) = 2x³ + 1. Determine whether the inverse of f is a function. Then find the inverse.

Solution

Example 8 :

Consider the function f(x) = 2√(x − 3). Determine whether the inverse of f is a function. Then find the inverse

Solution

Example 9 :

Find the inverse of the function that represents the surface area of a sphere, 

S = 4πr²

Then find the radius of a sphere that has a surface area of 100π square feet.

Solution

Example 10 :

The distance d (in meters) that a dropped object falls in t seconds on Earth is represented by

d = 4.9t²

Find the inverse of the function. How long does it take an object to fall 50 meters?

Solution

Example 11 :

The maximum hull speed v (in knots) of a boat with a displacement hull can be approximated by v = 1.34 √ℓ , whereℓ is the waterline length (in feet) of the boat. Find the inverse function. What waterline length is needed to achieve a maximum speed of 7.5 knots?

Solution

Example 12 :

Elastic bands can be used for exercising to provide a range of resistance. The resistance R (in pounds) of a band can be modeled by

R = (3/8) L − 5

where L is the total length (in inches) of the stretched band. Find the inverse function. What length of the stretched band provides 19 pounds of resistance?

Solution

Question 1 :

Suppose f(x) = 2x + 3.

(a) Evaluate f⁻¹(11).

(b) Find a formula for f⁻¹(y).

Solution

Question 2 :

Suppose the domain of f is the interval [0, 2], with f defined on this domain by the equation f(x) = x². 

(a) What is the range of f ?

(b) Find a formula for the inverse function f ⁻¹.

(c) What is the domain of the inverse function f ⁻¹?

(d) What is the range of the inverse function f ⁻¹?

Solution

Question 3 :

The surface area A (in square meters) of a person with a mass of 60 kilograms can be approximated by

A = 0.2195 h^0.3964

where h is the height (in centimeters) of the person.

a. Find the inverse function. Then estimate the height of a 60-kilogram person who has a body surface area of 1.6 square meters.

b. Verify that function A and the inverse model in part  (a) are inverse functions

Solution

Question 4 :

𝒇(𝒙) = 𝟐𝒙 − 𝟑

a) Determine 𝑓 −1 (𝑥)

b) Show that 𝑓(𝑓 ⁻¹ (𝑥)) = 𝑓 ⁻¹ (𝑓(𝑥)) = 𝑥

c) Graph 𝑓 𝑎𝑛𝑑 𝑓 −1

Solution

Question 5 :

Answer the following. Assume that f is a one-to-one function.

a)  f(4) = 5, find f^-1(5)

b)  f(3) = 9 and f(9) = 5, find f^-1(9)

Solution

Question 6 :

Use the graph of each function to graph its inverse function. 

f(x) = 3x + 1

Solution

Question 7 :

f(x) = (4x - 1)/(x - 1)

Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.