PRACTICE PROBLEMS ON CUBIC EQUATION USING SYNTHETIC DIVISION

Completely factor and find all zeros for each polynomial :

(1)  x³ + 4x² + 5x + 2

(2)  x⁴- x³ + 14x² - 16x - 32

(3)  5x³+29x²+19x-5

(4)  4x³ - 9x² + 6x - 1

(5)  3x⁴- 10x³ - 24x² - 6x + 5

(6)  3x³ + 9x² + 4x + 12

(7) Find the remainder of

f(x) = x³ + x² - 6x - 7 divided by x + 2

(8)  Find the value of a if x - 3is a factor of 

f(x) = x³ - 11x + a

(9)  Find the value of k if

f(x) = 3(x² + 3x - 4) - 8(x - k)

is divisible by x.

(10)  If -1 and 1 are two real roots of the polynomial function 

f(x) = ax³ + bx² + cx + d

and (0, 3) is the y-intercept of the graph of f, what is the value of b ?

Problem 1 :

x³ + 4x² + 5x + 2

Solution :

Let p(x)  =  x³ + 4x² + 5x + 2

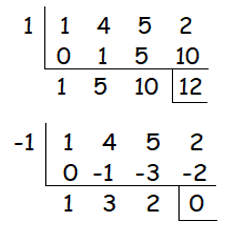
By dividing the cubic polynomial by 1, we get 12 ≠ 0.

Dividing by -1, we get 0 as remainder. So, -1 is one of the solutions.

From the bottom row, we create a quadratic polynomial. By factoring this, we will get two factors.

x²+3x+2  = (x+1) (x+2)

x³+4x²+5x+2  =  0

(x+1) (x+1) (x+2)  =  0

Equating each factor to zero, we get

x + 1  =  0, x + 1  =  0 and x + 2  =  0

x  =  -1, -1, -2

So, the solution is {-1, -1, -2}

Problem 2 :

x⁴- x³ + 14x² - 16x - 32

Solution :

Let p(x)  =  x⁴- x³ + 14x² - 16x - 32

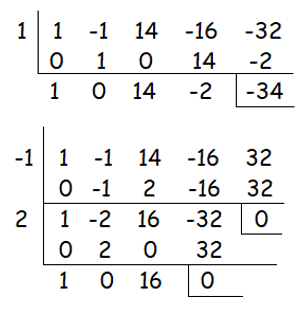
By dividing the fourth degree polynomial by 1, we get -34≠0.

By applying the value of x as -1 and 2, we get the remainder as 0.

So, the factors are (x+1) and (x–2)

So far we got two roots of the given polynomial.

By solving,

x² + 16  =  0

x²  =  -16

x  =  √-16

x  =  ±4i

So, it has a imaginary root.

x⁴- x³ + 14x² - 16x - 32

x + 1  =  0 and x - 2  =  0

x  =  -1, 2

So, the solution is {-1, 2, ±4i}

Problem 3 :

5x³+29x²+19x-5

Solution :

Let p(x)  =  5x³+29x²+19x–5

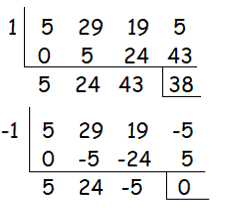
By dividing the cubic polynomial by 1, we get 38≠0. Dividing by -1, we get 0 as remainder. So, -1 is one of the solution.

By factoring quadratic polynomial 5x² + 24x – 5, we get

5x² + 24x - 5  =  (5x - 1) (x + 5)

(5x - 1) (x + 5)  =  0

Equating each factor to zero, we get

 x  =  -1, 1/5, -5

So, the solution is {-1, 1/5, -5}

Problem 4 :

4x³ - 9x² + 6x - 1

Solution :

Let p(x)  =  4x³ - 9x² + 6x - 1 

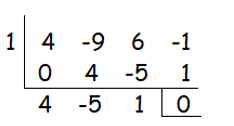
By dividing the cubic polynomial by 1, we get 0 as remainder. So, 1 is one of the zeroes of the polynomial.

By factoring quadratic polynomial 4x² - 5x + 1, we get

4x² - 5x + 1  =  (4x – 1) (x – 1)

The factors are (x – 1) (4x – 1) (x – 1)

Equating each factor to zero, we get

(x – 1) (4x – 1) (x – 1)  =  0

 x  =  1, 1/4, 1

So, the solution is {1, 1/4, 1}

Problem 5 :

3x⁴- 10x³ - 24x² - 6x + 5

Solution :

Let p(x)  =  3x⁴- 10x³ - 24x² - 6x + 5

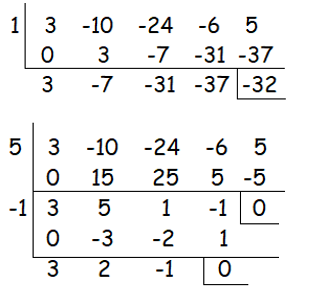
By dividing the fourth degree polynomial by 1, we get -32≠0. So dividing by 5, we get 0 as remainder,

Both x  =  5 and x  =  -1 are the two zeros of given polynomial.

By factoring quadratic polynomial 3x² + 2x - 1, we get

3x² + 2x - 1  =  (3x – 1) (x + 1)

Equating each factor to zero, we get

(3x – 1) (x + 1)  =  0

x  = 1/3, -1

So, the solution is {5, -1, 1/3, -1}

Problem 6 :

3x³ + 9x² + 4x + 12

Solution :

Let p(x)  =  3x³ + 9x² + 4x + 12

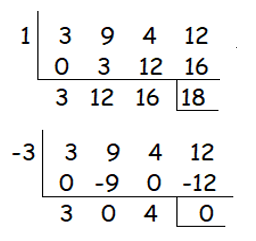
By dividing the cubic polynomial by 1, we get 18≠0. Dividing by -3, we get 0 as remainder. So, -3 is one of the zeroes of the given polynomial.

By solving,

3x² + 4 =  0

3x²  =  -4

x  =  √-4/3

x  =  ±2/√3i

So, the solution is {-3, ±2/√3i}.

Problem 7 :

Find the remainder of

f(x) = x³ + x² - 6x - 7 divided by x + 2

Solution :

x + 2 = 0

x = -2

f(x) = x³ + x² - 6x - 7

Applying x = -2 in the polynomial, we get

f(-2) = (-2)³ + (-2)² - 6(-2) - 7

= -8 + 4 + 12 - 7

= -15 + 16

= 1

So, the remainder is 1.

Problem 8 :

Find the value of a if x - 3 is a factor of 

f(x) = x³ - 11x + a

Solution :

f(x) = x³ - 11x + a

Since x - 3 is a factor, x - 3 = 0. Then x = 3,  and 3 is a zero of the polynomial.

f(3) = 3³ - 11(3) + a

0 = 27 - 33 + a

0 = -6 + a

a = 6

So, the value of a is 6.

Problem 9 :

Find the value of k if

f(x) = 3(x² + 3x - 4) - 8(x - k)

is divisible by x.

Solution :

f(x) = 3(x² + 3x - 4) - 8(x - k)

Since it is divisible by x, x = 0 is a solution.

f(0) = 3(0² + 3(0) - 4) - 8(0 - k)

0 = 3(-4) - 8(-k)

0 = -12 + 8k

8k = 12

k = 12/8

k = 3/2

So, the value of k is 3/2.

Problem 10 :

If -1 and 1 are two real roots of the polynomial function 

f(x) = ax³ + bx² + cx + d

and (0, 3) is the y-intercept of the graph of f, what is the value of b ?

Solution :

f(x) = ax³ + bx² + cx + d

Since -1 is a root, when x = -1, f(-1) = 0

Since 1 is a root, when x = 1, f(1) = 0

f(-1) = a(-1)³ + b(-1)² + c(-1) + d

0 = -a + b - c + d -------(1)

f(1) = a(1)³ + b(1)² + c(1) + d

0 = a + b + c + d -------(2)

The curve passes through the point (0, 3), then 

f(0) = a(0)³ + b(0)² + c(0) + d

3 = d

(1) + (2)

2b + 2d = 0

Applying d = 3, we get

2b + 2 (3) = 0

2b = -6

b = -3

So, the value of b is -3.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.