PRACTICE QUESTIONS FOR GRADE 10 MATH

Problem 1 :

The sum of ages of a father and the son is 45 years. Five years after the product of their ages will be 600. Find the present age of them.

Solution :

Let x and y be the present ages of father and son respectively.

x + y  =  45

y  =  45 - x  -----(1)

Five years after,

Age of father  =  x + 5 and age of son  =  y + 5

Five years after, the product of their ages  =  600

(x + 5)(y + 5)  =  600

(x + 5) (45 - x + 5)  =  600

(x + 5) (50 - x)  =  600

50x - x² + 250 - 5x  =  600

- x² + 45x + 250 - 600  =  0

- x² + 45x - 350  =  0

x² - 45x + 350  =  0

(x - 10) (x - 35)  =  0

x  =  10, x  =  35

x  =  10, then y  =  35

So, present age of son is 5 years and age of father is 35 years.

Problem 2 :

An over head tank has been constructed to supply water to a village with a population of 3140 at the rate of 25 liters per head per day. Water is pumped in to it through a pipe of 10 cm diameter, the rate of flow being 4 m per sec.How long will it take to fill the tank every morning?  (π = 3.14)

Solution :

Given : Population = 3140

Quantity = 25 liters per head

So total water supplied  =  25 ⋅ 3140 liters

Water supplied in 1 sec  =  π ⋅ (0.05)² ⋅ 4 cubic meter 

Water supplies in 1 sec = 22 ⋅  0.05 ⋅ 0.05 ⋅ 4/7

  =  (22 ⋅ 25 ⋅ 4)/(10000 ⋅ 7) cubic meter

  =  (2200 ⋅ 1000)/(10000 ⋅ 7) liters

  =  220/7 liters

So total time required = (25 ⋅ 3140)/(220/7) sec

  =  25 ⋅ 3140 ⋅ (7/220) sec

  =  2497 sec

  =  41 min 37 sec

Problem 3 :

It is 9 hours now in a 12 hour clock. What will be the time after 18 hours?

Solution :

9 + 18  =  27

27 - 24  =  3

It will be 3'o clock after 18 hours.

Problem 4 :

Find the sum of 15 cubes, whose sides are

1 cm, 2 cm, 3 cm ........... 15 cm respectively. 

Solution :

Sum of cubes (1³ + 2³ + 3³ + ....... + n³)

  =  [n(n + 1)/2]²

=  [15(15 + 1)/2]²

=  [15(8)]²

=  120²

=  14400 cm³

Problem 5 :

In a flower garden, there are 21 cactus plants in the first row, 19 in the second, 17 in the third and so on. There are 5 cactus plants in the last row. How many no of rows are there in the flower garden ?

Solution :

By writing the number of plants in each row as sequence, we get

21, 19, 17, ............5

n  =  [(l - a) / d]  + 1

n  =  [ (5 - 21)/(-2) ] + 1

n  =  8 + 1

n  =  9

So, the number of rows in the garden is 9.

Problem 6 :

A straight highway leads to the foot of a tower. A man is standing at the top of the tower observes a car at an angle of depression 30°, which is approaching the foot of a tower with a uniform speed. Six seconds after, the angle of depression of the car is found to be 60° find the time taken by a car to reach the foot of the tower from this point.

Solution :

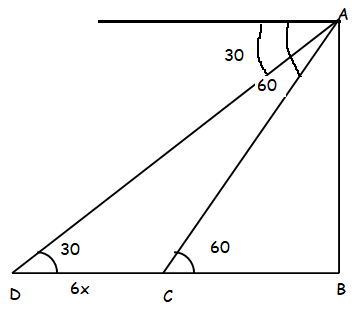
In triangle ADB,

tan θ  =  AB/(DC + BC)

tan 30  =  AB/(6x + BC)

1/√3  =  AB/(6x + BC)

AB  =  (6x + BC)/√3 ----(1)

In triangle ABC,

tan 60  =  AB/BC

√3  =  AB/BC

AB  =  BC√3 ----(2)

(1)  =  (2)

(6x + BC)/√3  =  BC√3

6x + BC  =  3BC

6x  =  2BC

BC  =  3x

So, time taken by the car to reach building is 3 seconds.

Problem 7 :

Find the area of the shaded region of the given picture.If the radius of the the two concentric circles with center O are 7 cm and 14 cm respectively and angle <AOB  =  40°.

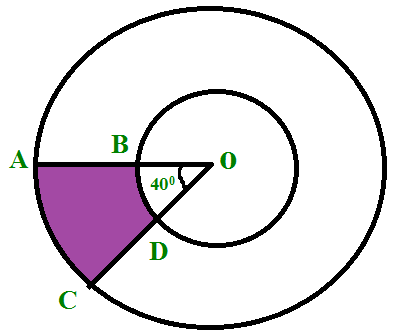
Solution :

Area of sector  =  (θ/360)πr²

   =  (40/360)π(14)² - (40/360)π(7)²

  =  (1/9)π (196 - 49)

  =  (1/9)π (147)

  =  (1/9) (22/7) (147)

  =  (1/9) ⋅ 22 ⋅ 21

  =  51.33 cm²

Area of the shaded region is 51.33 cm².

Problem 8 :

The straight lines x+y-5 = 0 and 2x+3y = 13 are the diameters of a circle. Find the radius of the circle if the circle passes through the point (2, 1).

Solution :

By finding point of intersection of diameter, we get the centre of the circle.

x+y = 5  ----(1)

2x+3y = 13  ----(2)

(1) ⋅ 2 ==> 2x + 2y  =  10

(1)- (2)   -2x - 3y  =  -13

              --------------------

             -y  =  -3

y  =  3

By applying the value of in (1), we get

x + 3  =  5

x  =  2

Center is (2, 3).

The circle is passing through the point (2, 1).

Distance between the points (2, 3) and (2, 1)

  =  √(x₂ - x₁)² + (y₂ - y₁)²

  =  √(2 - 2)² + (3 - 1)²

  =  √4

=  2

So, the radius of the circle is 2 cm.

Problem 9 :

The variance of 5 values is 9. If each value is doubled then determine the standard deviation of new values. 

Solution :

Standard deviation  =  √variance

We should remember the point that if every value is multiplied or divided by by the same number, the standard deviation changes by that number. 

So, standard deviation of new values  =  √9

  =  3

Problem 10 :

The mean runs scored by three batsman A,B and C in the same series of 10 innings are 58,48 and 14 respectively. The standard deviation of their runs are 15,12 and 2 respectively.Who is the most consistent batsman?

Solution :

By finding coefficient of variation, we come to know who is the consistent batsman.

Coefficient of variation  = (σ/x̅) ⋅ 100%

CV of batsman A :

  =  (15/58) ⋅ 100%

  =  25.86%

CV of batsman B :

  =  (11/48) ⋅ 100%

  =  22.91%

CV of batsman C :

  =  (2/14) ⋅ 100%

  =  14.28%

So, batsman A is consistent player.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.