PRACTICE QUESTIONS ON SIMILAR TRIANGLES

Question 1 :

Check if the triangle given below is similar.

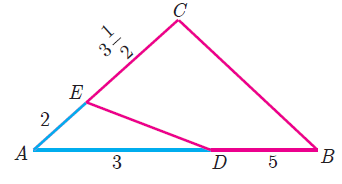
Solution : 

Let us consider the triangles, AED and ACB

If two triangles are similar, then the ratio of its corresponding sides will be equal.

Condition :

AE/AC  =  AD/AB

2/(7/2)  ≠  3/5

4/7  ≠  3/5

So, the triangles AED and ACB are not similar.

Question 2 :

Find the value of x in the picture given below.

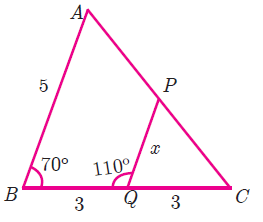
In triangle PQC,

<PQC  =  180 - 110

<PQC  =  70

Now let us consider the triangles ABC and PQC.

<ABC  =  <PQC

<ACB  =  <PCQ

By using AA criterion, the above triangles are similar. Hence the ratio of their corresponding sides will be equal.

AB/PQ  =  BC/QC

5/x  =  (3+3)/3

5/x  =  6/3

5/x  =  2

x  =  5/2  =  2.5

Question 3 :

A girl looks the reflection of the top of the lamp post on the mirror which is 6.6 m away from the foot of the lamppost. The girl whose height is 1.25 m is standing 2.5 m away from the mirror. Assuming the mirror is placed on the ground facing the sky and the girl, mirror and the lamppost are in a same line, find the height of the lamp post.

Solution :

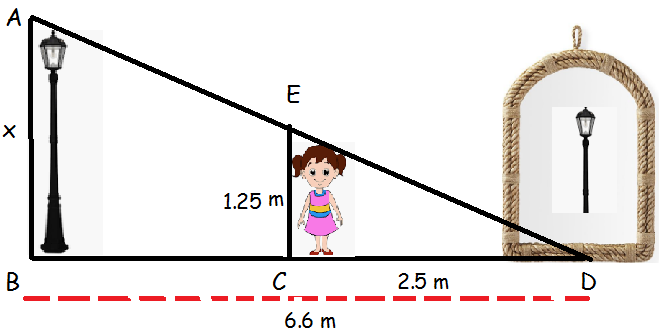
In triangles ABD and CED

<ABD  =  <ECD

<ADB  =  <EDC

By AA the above triangles are similar,

AB/ EC  =  BD/CD

x/1.25  =  6.6/2.5

x  =  6.6(1.25)/2.5

x  =  3.3 m

Hence the height of the lamp post is 3.3 m.

Question 4 :

A vertical stick of length 6 m casts a shadow 400 cm long on the ground and at the same time a tower casts a shadow 28 m long. Using similarity, find the height of the tower.

Solution :

Let us draw a rough diagram based on the given information.

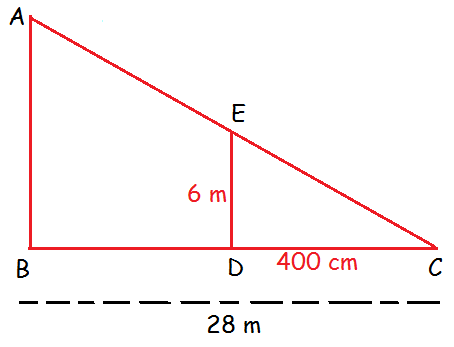
AB/ED  =  BC/DC

400 cm  =  4 m

AB/6  =  28/4

AB  =  (28/4)(6)

AB  =  42 m

Hence the height of the tower is 42 m.

Question 5 :

Two triangles QPR and QSR, right angled at P and S respectively are drawn on the same base QR and on the same side of QR. If PR and SQ intersect at T, prove that PT × TR = ST × TQ.

Solution :

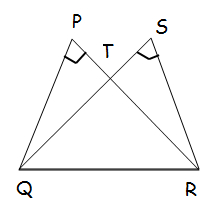
In triangles PTQ, and STR

<QPT  =  <RST  (A)

<PTQ  =  <STR (Vertically opposite angles)  (A) 

So, the triangles PTQ and STR are similar.

PQ/SR  =  PT/TS  =  QT/RT

PT/TS  =  QT/RT

PT x RT  =  QT x TS

Hence proved.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.