PROBLEMS INVOLVING ANGLE BISECTOR THEOREM
Angle bisector :
An angle bisector is a line segment, ray, or line that divides an angle into congruent adjacent angles.
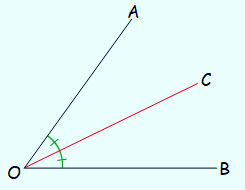
In the above figure, line segment OC bisects <AOB.
So, <AOC = <BOC which means <AOC and <BOC are congruent angles.
BD bisects <ABC. Find the value of x :
Example 1 :
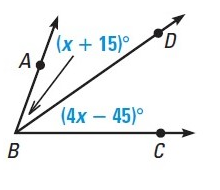
Solution :
In the given figure, BD bisects <ABC
So, <ABD = <CBD
(x + 15)˚
= (4x – 45)˚
x + 15˚ = 4x - 45˚
x – 4x = -45 – 15
-3x = -60
x = 20˚
So, the value of x is 20˚
Example 2 :
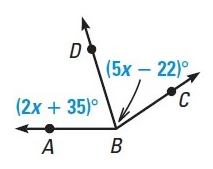
Solution :
In the given figure, BD bisects <ABC
So, <ABD = <CBD
(2x + 35)˚ = (5x – 22)˚
2x + 35˚ = 5x - 22˚
2x – 5x = -35 – 22
-3x = -57
x = 19˚
So, the value of x is 19˚
Example 3 :
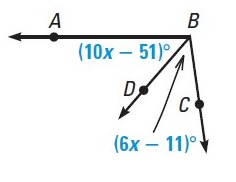
Solution :
In the given figure, BD bisects <ABC
So, <ABD = <CBD
(10x - 51)˚ = (6x – 11)˚
10x - 51˚ = 6x - 11˚
10x – 6x = 51˚ – 11˚
4x = 40˚
x = 10˚
So, the value of x is 10˚
Example 4 :
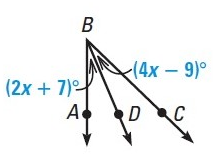
Solution :
In the given figure, BD bisects <ABC
So, <ABD = <CBD
(2x + 7)˚
= (4x – 9)˚
2x + 7˚ = 4x - 9˚
2x – 4x = -7 – 9
-2x = -16
x = 8˚
So, the value of x is 8˚
Example 5 :
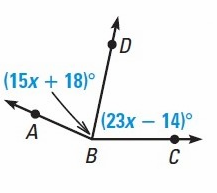
Solution :
In the given figure, BD bisects <ABC
So, <ABD = <CBD
(15x + 18)˚ = (23x – 14)˚
15x + 18˚ = 23x - 14˚
15x – 23x = -18 – 14
-8x = -32
x = 4˚
So, the value of x is 4˚
Example 6 :
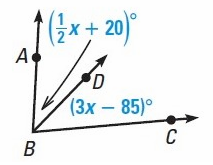
Solution :
In the given figure, BD bisects <ABC
So, <ABD = <CBD
(1/2x + 20)˚ = (3x – 85)˚
1/2x + 20˚ = 3x - 85˚
1/2x – 3x = -20 – 85
-5/2x = -105
5x = 210
x = 42˚
So, the value of x is 42˚
Example 7 :
The bisector of <A of the triangle ABC meets BC at D and BC is produced to E. Prove that <ABC + <ACE = 2 <ADC
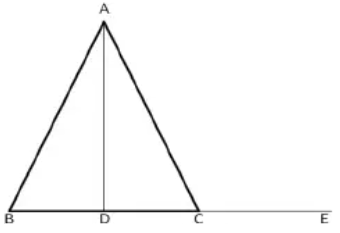
Solution :
Since AD is the bisector of <BAC,
<BAD = <DAC = x
<ACE = exterior angle
= sum of remote interior angles
Let <ABC = y ------(1)
<ABC + <BAC = <ACE
y + 2x = <ACE
<ACE = 2x + y ------(2)
(1) + (2)
<ABC + <ACE = y + 2x + y
= 2y + 2x
= 2(x + y)
= 2 (<BAD + <ABC)
Example 8 :
The line segment joining the midpoint of any side of with opposite vertex is
a) altitude b) median c) Perpendicular bisector
d) angle bisector
Solution :
Midpoint of line segment will be at the middle exactly. The line segment joining the midpoint of any side of the opposite vertex is at median.
Example 9 :
Triangles ABC and DBC are two isosceles triangles on the same base BC and their vertices A and D are also on the same side of BC. If AD is extended to intersect BC at P, show that
(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects angles BAC and BDC
(iv) AP is the perpendicular bisector of BC
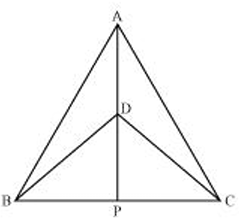
Solution :
(i)
Triangle ABD and ACD are isosceles triangles. Then AB and AC are congruent sides.
AB = AC
AD is common
Since BDC is an isosceles triangle, BD = DC
Then, ∆ABD ≅ ∆ACD
(ii)
In triangle ABP and ACP,
AB = AC
AP is common
<ABP = <ACP
Then, ∆ABP ≅ ∆ACP
(iii) Using CPCTC, from the above proof
<BAP = <CAP
<BDP = <CDP
Then AP bisects angles BAC and BDC.
(iv)
<BPD + <CPD = 180
Since DBP and DCP are congruent, then
<BPD = <CPD (by CPCTC)
<BPD + <BPD = 180
2<BPD = 180
<BPD = 90
Then AP is the perpendicular bisector of BC.
Example 10 :
In quadrilateral ABCD, AC = AD and AB bisects <A and triangle ABC
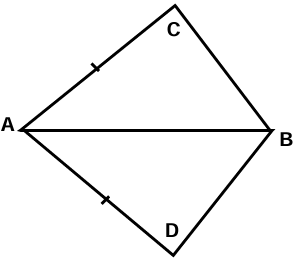
a) BC > BD b) BC < BD
c) BC = BD d) BC = (1/2 )BD
Solution :
In triangles ACB and ADB
<CAB = <DAB (AB bisects <CAD)
AC = AD (Given)
AB = AB (Common)
Then, triangles ACB and ADB are congruent. Here BC and BD are corresponding sides of congruent triangles. So, BC = BD.
Example 11 :
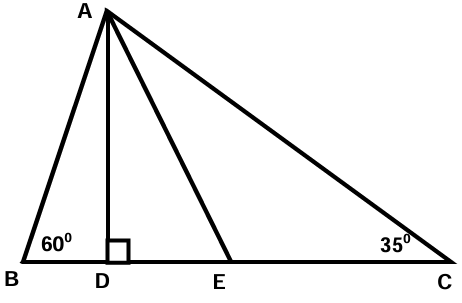
In the given figure AD is perpendicular to BC. AE is the angle bisector of <BAC. Find <DAE.
Solution :
In triangles ABD,
<BDA = 90, <DBA = 60 and <BAD = 30
In triangle ADC,
<ADC + <DCA + <DAC = 180
90 + 35 + <DAC = 180
<DAC = 180 - 125
<DAC = 55
<DAE = <DAC / 2
= 55/2
= 27.5
Example 12 :
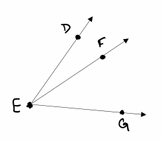
EF is the bisector of DEG(not drawn in scale). If <DEF = 3x + 1 and <DEG = 5x + 19 , find the value of x.
Solution :
<DEF = 3x + 1 and <DEG = 5x + 19
<DEG / 2 = <DEF
(5x + 19)/2 = 3x + 1
5x + 19 = 2(3x + 1)
5x + 19 = 6x + 3
19 - 3 = 6x - 5x
16 = x
So, the value of x is 16.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus AB Problems with Solutions (Part - 10)
Feb 11, 25 11:15 AM
AP Calculus AB Problems with Solutions (Part - 10) -
AP Calculus AB Problems with Solutions (Part - 11)
Feb 11, 25 11:09 AM
AP Calculus AB Problems with Solutions (Part - 11) -
AP Calculus AB Problems with Solutions (Part - 9)
Feb 10, 25 06:02 PM
AP Calculus AB Problems with Solutions (Part - 9)