PROBLEMS ON INTERIOR AND EXTERIOR ANGLES OF TRIANGLE

Problem 1 :

In triangle PQR, the measure of ∠P is 36. The measure of ∠Q is five times the measure of ∠R. Find ∠Q and ∠R.

Solution :

∠P = 36

∠Q = 5∠R

In triangle PQR, the sum of interior angles is 180°.

∠P + ∠Q + ∠R = 180°

36° + 5∠R + ∠R = 180°

6R + 36° = 180°

Subtract 36° from both sides.

6∠R = 144°

Divide both sides by 6.

∠R = 24°

∠Q = 5∠R

∠Q = 5(24°)

∠Q = 120°

Problem 2 :

The exterior angle of a triangle is 120°. Find the value of x if the opposite non-adjacent interior angles are (4x + 40)° and 60°.

Solution :

Using Exterior Angle Theorem,

(4x + 40)° + 60° = 120°

4x + 40 + 60 = 120

4x + 100 = 120

Subtract 100 from both sides.

4x = 20

Divide both sides by 4.

5 = x

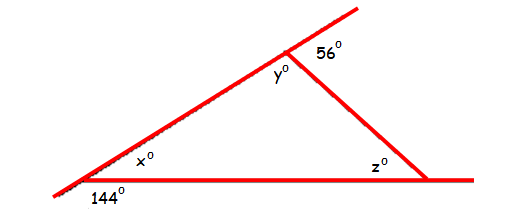
Problem 3 :

Find the values of x, y and z.

Solution :

x° + z° = 56° ----(1)

y° and 56° are linear pair.

y° + 56° = 180°

Subtract 56 from both sides.

y = 124

x° and 144° are linear pair.

x° + 144° = 180°

Subtract 144 from both sides.

x = 36

Substitute x = 36 in (1).

36 + z = 56

Subtract 36 from both sides.

z = 20

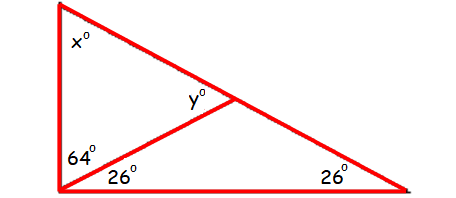
Problem 4 :

Find the values of x, y and z.

Solution :

Using Exterior Angle Theorem,

y° = 26° + 26°

y = 52

By Angle Sum Property of Triangle,

x° + y° + 64° = 180°

X + 52 + 64 = 180

x + 116 = 180

Subtract 116 from both sides.

x = 64

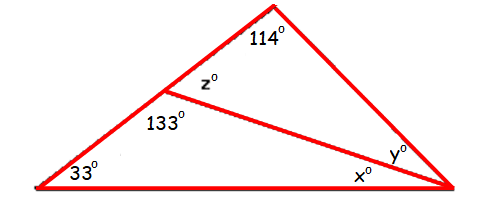
Problem 5 :

Solution :

Using Exterior Angle Theorem,

x° + 33° = z°

x + 33 = z ----(1)

z° and 133° are linear pair.

z + 133 = 180

Subtract 133 from both sides.

z = 47

Substitute z = 47 in (1).

x + 33 = 47

Subtract 33 from both sides.

x = 14

By Angle Sum Property of Triangle,

y° + z° +114° = 180°

y + z + 114 = 180

Subtract 114 from both sides.

y + z = 66

Substitute z = 47.

y + 47 = 66

y = 19

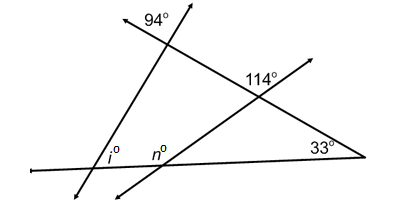
Problem 6 :

Find the values of i and n.

Solution :

Vertically opposite angles are equal.

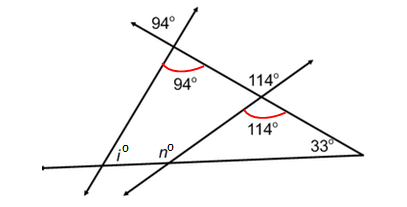
Using Exterior Angle Theorem,

n° = 114° + 33°

n = 147

By Angle Sum Property of Triangle,

94° + i° + 33° = 180°

i + 127 = 180

Subtract 127 from both sides.

i = 53

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.