PROBLEMS ON PROPERTIES OF ODD AND EVEN NUMBERS

Odd Number :

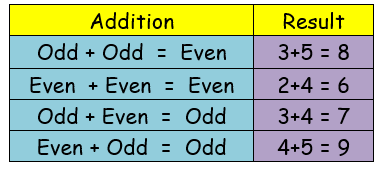
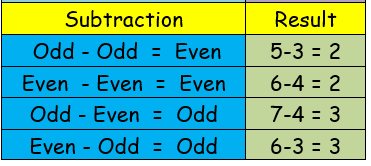
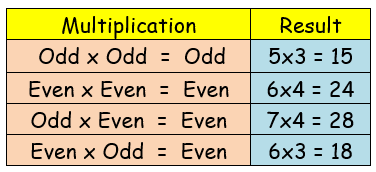
Any integer that cannot be divided exactly by 2 is an odd number.

Even Number :

Any integer that can be divided exactly by 2 is an even number. The last digit is 0, 2, 4, 6 or 8

Example 1 :

The sum of three even numbers

Solution :

Let us take any 3 even numbers.

For example,

If a  =  2, b  =  4 and c  =  6

The sum of three even numbers  =  2+4+6

=  12

12 is even number.

So, sum of three even numbers is even.

Example 2 :

The sum of three odd numbers

Solution :

Let us take any 3 odd numbers.

For example,

If a  =  1, b  =  3 and c  =  7

The sum of three odd numbers  =  1+3+7

=  11

11 is odd number.

So, sum of three odd numbers is odd.

Example 3 :

The product of an even and two odd numbers

Solution :

Let us take an even number and two odd numbers.

For example,

If even number is 4, then odd numbers are 3 and 7.

product  =  4 × (3 × 7)

=  4 × 21

=  84

84 is even number.

So, product of even and two odd numbers is even.

Example 4 :

The sum of four consecutive odd numbers.

Solution :

If x be the first odd number, then four consecutive odd integers are

x, x + 2, x + 4, x + 6.

Sum of four consecutive odd numbers  

=  x+(x+2)+(x+4)+(x+6)

=  4x+12

=  4(x+3)

x is odd 3 is also odd, sum of odd and odd will given even number and product of even and even is even.

Example 5 :

(even)³ means ‘an even number is raised to the power 3’. Which of these are odd and which are even ?

(i)  (even)²    (ii)  (odd)²   (iii)  (even)³   (iv)  (odd)³

(v)  (even)⁴    (vi)  (odd)⁴

Solution :

(i)  (even)²

(even)²  =  even × even

=  even

(ii)  (odd)²

(odd)²  =  odd × odd

=  odd

(iii)  (even)³

(even)³  =  even × even × even

=  even × even

=  even

(iv)  (odd)³

(odd)³  =  odd × odd × odd

 =  odd × odd

=  odd

(v)  (even)⁴

(even)⁴  =  even × even × even × even

=  even × even

=  even

(vi)  (odd)⁴

(odd)⁴  =  odd × odd × odd × odd

=  odd × odd

=  odd

Example 6 :

What is the smallest positive whole number which when increased by 1, is divisible by 3, 4 and 5 ?

Solution :

By finding the least common multiple of 3, 4 and 5, we get 60.

60 is exactly divisible by 3, 4 and 5.

So, the required number is 59.

Example 6 :

The product of seven consecutive even integers is 0. What is the least possible value of any one of these integers?

(A) -14    (B) -12    (C) -10    (D) -8    (E) -6

Solution :

Since the product of 7 consecutive even numbers is 0, one of the numbers must be 0

If we start with -14, the seven consecutive numbers will be

-14, -12, -10, -8, -6, -4, -2

Here we cannot include 0. Then the product will not become 0. 

Then the answer is -12.

Example 7 :

If x and y are positive integers and (xy + x) is even, which of the following must be true?

(A) If x is odd, then y is odd. 

(B) If x is odd, then y is even.

(C) If x is even, then y is odd.

(D) If x is even, then y is even.

(E) x cannot be odd

Solution :

= (xy + x)

Option A :

If x is odd, let x = 3

If y is odd, let x = 5

= (3(5) + 3)

= 15 + 3

= 18

It is even. Then option A is correct.

Example 8 :

The square of which of the following would be even number ?

A)  521     B) 322    C)  1237    D)  923

Solution :

Using the properties of odd and even numbers, the product of 

• even x even = even
• even x odd = even
• odd x even = even
• odd x odd = odd

In option B, 322 is even. Multiplying two even numbers we will get even number. Then option B is correct.

Example 9 :

If x and y be positive integers such that x is prime and y is composite. Then

A)  y - x cannot be even number

B)  (x + y)/x cannot be an even number

C)  x + y cannot be even

D)  None of these statements are true

Solution :

Let us assume x = 3 and y = 10

Option A :

y - x = 10 - 3 ==> 7 cannot be even

Option B :

(x + y)/x

= (3 + 10)/3

= 13/3

Cannot be even.

Option C :

x + y = 10 + 3

adding even number by odd, we will get odd. Then, 

= 13 cannot be even

So, the answer is no statements is true. Option D is correct.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.