PROBLEMS ON TRAINS WITH SOLUTIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
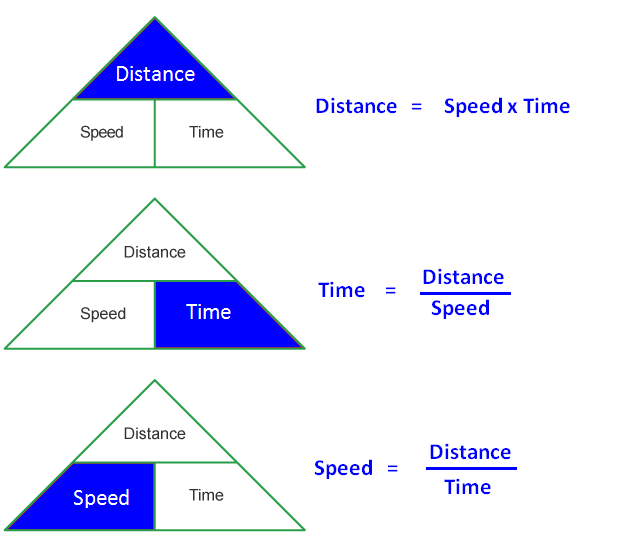
1. To convert the speed km per hour to meter per speed, multiply 5/18.
2. To convert the speed meter per second to km per hour, multiply 5/18.
3. Let the length of the train be L meters.
Distance traveled to pass a standing man = L meters
Distance traveled to pass a pole = L meters
4. Let the length of the train be 'a' meters and the length of the platform be 'b' meters.
Distance traveled to pass the platform is (a + b) meters
5. If two trains are moving on the same directions with speed of 'p' m/sec and 'q' m/sec (here p > q), then their relative speed is
= (p - q) m/sec
6. If two trains are moving opposite to each other in different tracks with speeds of 'p' m/sec and 'q' m/sec, then their relative speed is
= (p + q) m/sec
7. Let 'a' and 'b' are the lengths of the two trains.
They are traveling on the same direction with the speed 'p' m/sec and 'q' m/sec (here p > q), then the time taken by the faster train to cross the slower train
= (a + b)/(p - q) seconds
8. Let 'a' and 'b' are the lengths of the two trains.
They are traveling opposite to each other in different tracks with the speed 'p' m/sec and 'q' m/sec, then the time taken by the trains to cross each other
= (a + b)/(p + q) seconds
9. Two trains leave at the same time from the stations P and Q and moving towards each other.
After crossing, they take 'p' hours and 'q' hours to reach Q and P respectively.
Then the ratio of the speeds of two trains is √q : √p.
10. Two trains are running in the same direction/opposite direction.
The person in the faster train observes that he crosses the slower train in 'm' seconds.
Then the distance covered in 'm' seconds in the relative speed is
= length of the slower train
11. Two trains are running in the same direction/opposite direction.
The person in the slower train observes that the faster train crossed him 'm' seconds.
Then the distance covered in 'm' seconds in the relative speed is
= length of the faster train
Problem 1 :
If the speed of a train is 20 m/sec, find the speed the train in km/hr.
Solution :
speed = 20 m/sec
To convert m/sec to km/h, multiply the given m/sec by 18/5.
= 20 x 18/5 km/hr
= 72 km/hr
Problem 2 :
The length of a train is 300 meter and length of the platform is 500 meter. If the speed of the train is 20 m/sec, find the time taken by the train to cross the platform.
Solution :
Distances needs to be covered to cross the platform is
= sum of the lengths of the train and platform
= 300 + 500
= 800 meters
Time taken to cross the platform is
= distance/speed
= 800/20
= 40 seconds
Problem 3 :
A train is running at a speed of 20 m/sec. If it crosses a pole in 30 seconds, find the length of the train in meters.
Solution :
The distance covered by the train to cross the pole is
= length of the train
Given : Speed is 20 m/sec and time taken to cross the pole is 30 seconds.
distance = speed ⋅ time
length of the train = speed ⋅ time
= 20 ⋅ 30
= 600 meters
Problem 4 :
It takes 20 seconds for a train running at 54 km/h to cross a platform. And it takes 12 seconds for the same train in the same speed to cross a man walking at the rate of 6 km/h in the same direction in which the train is running. What is the length of the train and length of platform (in meters).
Solution :
Relative speed of the train to man = 54 - 6 = 48 km/hr.
= 48 ⋅ 5/18 m/sec
= 40/3 m/sec
When the train passes the man, it covers the distance which is equal to its own length in the above relative speed.
Given : It takes 12 seconds for the train to cross the man
So, the length of the train = relative speed x time
= (40/3) ⋅ 12
= 160 m
Speed of the train = 54 km/h
= 54 ⋅ 5/18 m/sec
= 15 m/sec
When the train crosses the platform, it covers the distance which is equal to the sum of lengths of the train and platform
Given : The train takes 20 seconds to cross the platform.
So, the sum of lengths of train and platform
= speed of the train ⋅ time
= 15 x 20
= 300 meters
length of train + length of platform = 300
160 + length of platform = 300
length of platform = 300 - 160
= 140 meters
Hence the lengths of the train and platform are 160 m and 140 m respectively.
Problem 5 :
Two trains running at 60 km/h and 48 km/h cross each other in 15 seconds when they run in opposite direction. When they run in the same direction, a person in the faster train observes that he crossed the slower train in 36 seconds. Find the length of the two trains (in meters).
Solution :
When two trains are running in opposite direction,
relative speed = 60 + 48
= 108 km/h
= 108 ⋅ 5/18 m/sec
= 30 m/sec
Sum of the lengths of the two trains is sum of the distances covered by the two trains in the above relative speed.
Then, sum of the lengths of two trains is
= speed ⋅ time
= 30 ⋅ 15
= 450 m
When two trains are running in the same direction,
relative speed = 60 - 48
= 12 km/h
= 12 ⋅ 5/18
= 10/3 m/sec
When the two trains running in the same direction, a person in the faster train observes that he crossed the slower train in 36 seconds.
The distance he covered in 36 seconds in the relative speed is equal to the length of the slower train.
length of the slower train = 36 ⋅ 10/3 = 120 m
length of the faster train = 450 - 120 = 330 m
Hence, the length of the two trains are 330 m and 120 m.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 42)
Dec 30, 25 05:52 AM
10 Hard SAT Math Questions (Part - 42) -
10 Hard SAT Math Questions (Part - 38)
Dec 29, 25 04:21 AM
10 Hard SAT Math Questions (Part - 38) -
10 Hard SAT Math Questions (Part - 39)
Dec 28, 25 11:20 PM
10 Hard SAT Math Questions (Part - 39)
