PRODUCT RULE OF LOGARITHMS

Before learning the product rule of logarithms, we have to be aware of the parts of a logarithm.

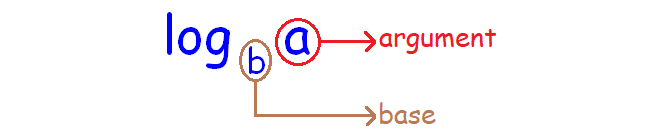
Consider the logarithm given below.

log_ba

In the logarithm above, 'a' is called argument and 'b' is called base.

Product Rule of Logarithm

Logarithm of product of two numbers is equal to the sum of the logarithms of the numbers to the same base.

log_amn = log_am + log_an

In other words, we can simplify the addition of two logarithms, if the they have the same base. That is, if two logarithms with same base are in addition, we can write single logarithm with the given base and the argument is the product of two arguments.

log_xa + log_xb = log_xab

Apart from the product rule of logarithms, there are two other important rules of logarithm.

(i) Quotient Rule

(ii) Power Rule

Quotient Rule of Logarithms

Logarithm of the quotient of two numbers is equal to the difference of their logarithms to the same base.

log_a(m/n) = log_am - log_an

Power Rule of Logarithms

Logarithm of a number raised to a power is equal to the power multiplied by the logarithm of the number to the same base.

log_amⁿ = nlog_am

Video Lesson

Solved Problems

Problem 1 :

Find the logarithm of 125 to the base 5.

Solution :

Write 125 as a power of 5.

125 = 5 x 5 x 5

= 5³

log₅125 = log₅(5)³

= 3log₅5

= 3(1)

= 3

Problem 2 :

Find the logarithm 1728 to the base 2√3.

Solution :

Write 1728 as a power of 2√3.

1728 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3 x 3

1728 = 2⁶ x 3³

1728 = 2⁶ x [(√3)²]³

1728 = 2⁶ x (√3)⁶

1728 = (2√3)⁶

log_2√3(1728) = log_2√3(2√3)⁶

Using the power rule of logarithms,

= 6log_2√3(2√3)

= 6(1)

= 6

Problem 3 :

Find the logarithm of 0.001 to the base 0.1.

Solution :

log_0.10.001 = log_0.1(0.1)³

= 3log_0.10.1

= 3(1)

= 3

Problem 4 :

Find the logarithm 1/64 to the base 4.

Solution :

log₄(1/64) = log₄1 - log₄64

= 0 - log₄(4)³

= -3log₄4

= -3(1)

= -3

Problem 5 :

Find the logarithm of 0.3333...... to the base 3.

Solution :

log₃(0.3333......) = log₃(1/3)

= log₃1 - log₃3

= 0 - 1

= -1

Problem 6 :

If log_y(√2) = 1/4, find the value of y.

Write the equation in exponential form.

√2 = y^1/4

Raise to the power 4 on both sides.

(√2)⁴ = (y^1/4)⁴

(2^1/2)⁴ = y

2² = y

4 = y

Problem 7 :

Simplify :

(1/2)log₁₀25 - 2log₁₀3 + log₁₀18

Solution :

= (1/2)log₁₀25 - 2log₁₀3 + log₁₀18

Using power rule of logarithms,

= log₁₀25^1/2 - log₁₀3² + log₁₀18

= log₁₀(5²)^1/2 - log₁₀3² + log₁₀18

= log₁₀5 - log₁₀9 + log₁₀18

= log₁₀5 + log₁₀18 - log₁₀9

Using the product rule of logarithms,

= log₁₀(5 x 18) - log₁₀9

= log₁₀90 - log₁₀9

Using the quotient rule of logarithms,

= log₁₀(90/9)

= log₁₀10

= 1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.