PROJECTION OF VECTOR a ON b

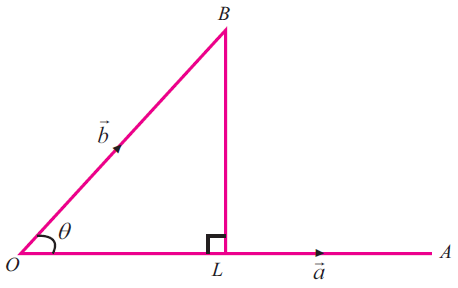
Let OA  = a vector , OB vector = b vector and q be the angle between a vector and b vector.

Draw BL perpendicular to OA. From the right triangle OLB

cos θ  =  OL/OB

OL  =  OB cos θ  == |b| cos θ 

But OL is the projection of b vector on a vector.

a vector . b vector  =  |a vector| |b vector| cosθ 

  =  |a vector| OL

a vector . b vector  = |a| (projection of b on a)

Question 1 :

Find the projection of the vector i vector + 3j vector  + 7k vector on the vector 2i vector + 6j vector  + 3k vector.

Solution :

a vector  =  (i + 3j + 7k) vector

b vector  =  (2i + 6j + 3k) vector

Projection of a vector on b vector  =  (a . b) / |b vector|

a vector . b vector  =  1(2) + 3(6) + 7(3)

  =  2 + 18 + 21

  =  41

|b vector|  =  √(2² + 6² + 3²)   =  √49  =  7

Projection of a vector on b vector  =  41/7

Question 2 :

Find λ, when the projection of a = λ i + j + 4k on b = 2i + 6 j + 3k is 4 units.

Solution :

Projection of a vector on b vector  =  (a . b) / |b vector|

a = λ i + j + 4k on b = 2i + 6 j + 3k 

a . b  = λ(2) + 1(6) + 4(3)  =  4

2λ + 6 + 12  =  4

 2λ + 18  =  4

2λ  =  4 - 18

2λ  =  -14

λ  =  -14/2  =  -7

Hence the value of λ is -7.

Question 3 :

Three vectors a vector, b vector and c vector are such that |a vector|= 2, |b vector| = 3,|c vector| = 4 , and a vector + b vector + c vector = 0 . Find 4 a . b + 3b . c + 3c . a.

Solution :

a vector + b vector + c vector  =  0

a vector + b vector  =  - c vector

|a vector + b vector|  =  |-c vector|

|a vector + b vector|²  =  |-c vector|²

|avector|²+|bvector|²+ 2 a . b =|c vector|²

4 + 9 + 2 (a . b)   =  16

13 + 2 (a . b)   =  16

2 (a . b)   =  16 - 13

2 (a . b)   =  3

4  a . b   =  6  -----(1)

||| ly

|a vector|²+|c vector|²+ 2 a . c =|b vector|²

4 + 16 + 2 (a . c)   =  9

20 + 2 (a . c)   =  9

2 (a . c)   =  9 - 20

2 (a . c)   =  -11

a . c   =  -11/2

3 a . c  =  -33/2 -----(2)

||| ly

|b vector|²+|c vector|²+ 2 b . c =|a vector|²

9 + 16 + 2 (b . c)   =  4

25 + 2 (b . c)   =  4

2 (b . c)   =  4 - 25

2 (b . c)   =  -21

b . c   =  -21/2

3 b . c  =  -63/2 -----(3)

4 a . b + 3 b . c + 3 c . a   =  6 - (63/2) - (33/2)

=  (12 - 63 - 33)/2

=  (12 - 96)/2

=  -  84/2

=  -42

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.