PROPERTIES OF PARALLELOGRAM

A parallelogram is a quadrilateral with both pairs of opposite sides parallel. When we mark diagrams of quadrilaterals, use matching arrowheads to indicate which sides are parallel.

For example, in the diagram shown below,

AB || CD

AD || BC

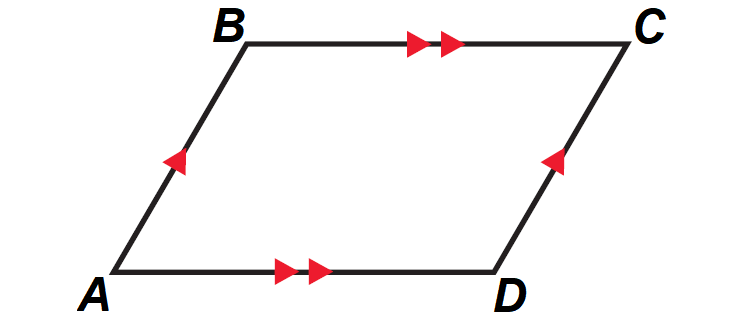
Properties of Parallelogram

Property 1 :

If a quadrilateral is a parallelogram, then its opposite sides are congruent.

It has been illustrated in the diagram shown below.

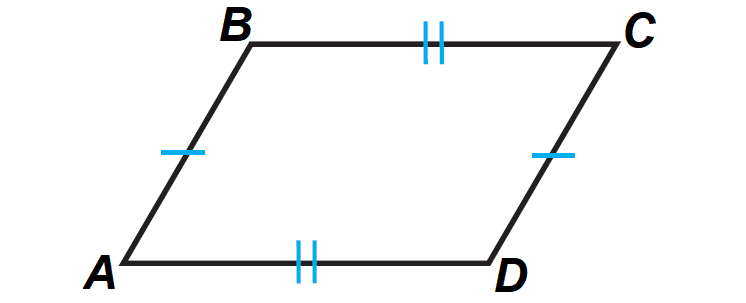
In the diagram above,

AB ≅ DC

AD ≅ BC

Property 2 :

If a quadrilateral is a parallelogram, then its opposite angles are congruent.

It has been illustrated in the diagram shown below.

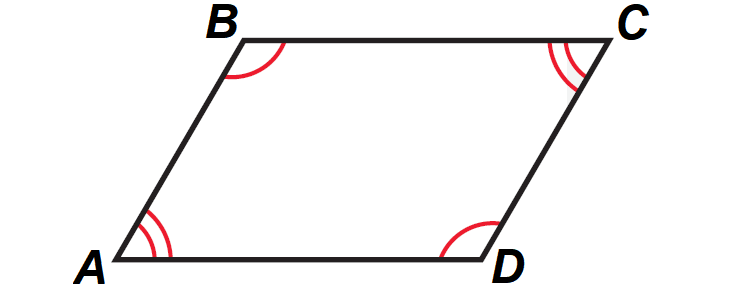
In the diagram above,

m∠A ≅ m∠C

m∠B ≅ m∠D

Property 3 :

If a quadrilateral is a parallelogram, then its consecutive angles are supplementary.

It has been illustrated in the diagram shown below.

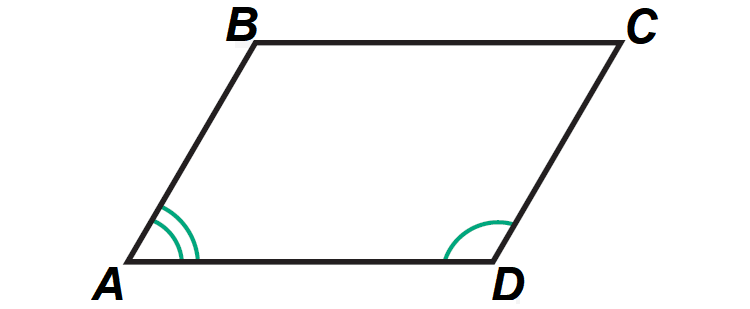
In the diagram above,

m∠A + m∠B = 180°

m∠B + m∠C = 180°

m∠C + m∠D = 180°

m∠A + m∠D = 180°

Property 4 :

If a quadrilateral is a parallelogram, then its diagonals bisect each other.

It has been illustrated in the diagram shown below.

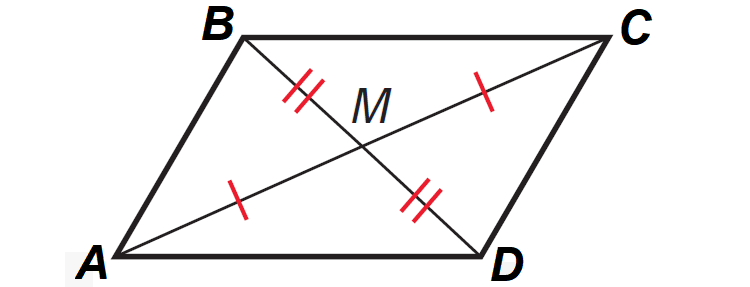
In the diagram above,

AM ≅ CM

BM ≅ DM

Solving Problems Using Properties of Parallelogram

Problem 1 :

Find the lengths of SR and SK in the parallelogram shown below. Explain your reasoning.

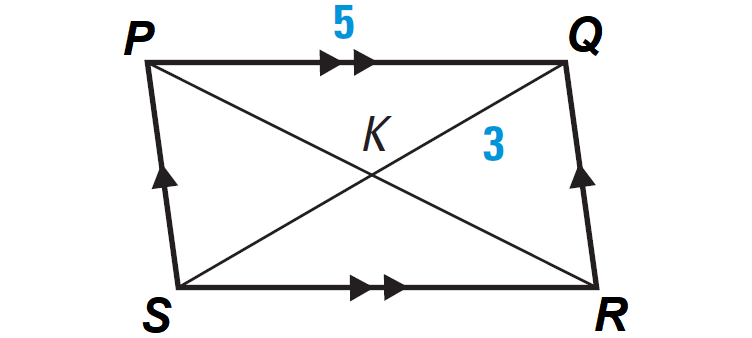
Solution :

Finding the length of SR :

By Theorem, opposite sides of a parallelogram are congruent.

So, we have

SR = PQ

From the diagram, PQ = 5.

SR = 5

Finding the length of SK :

By Theorem, diagonals of a parallelogram bisect each other.

So, we have

SK = QK

From the diagram, QK = 3.

SK = 3

Problem 2 :

Find the measures of ∠C and ∠B in the parallelogram ABCD.

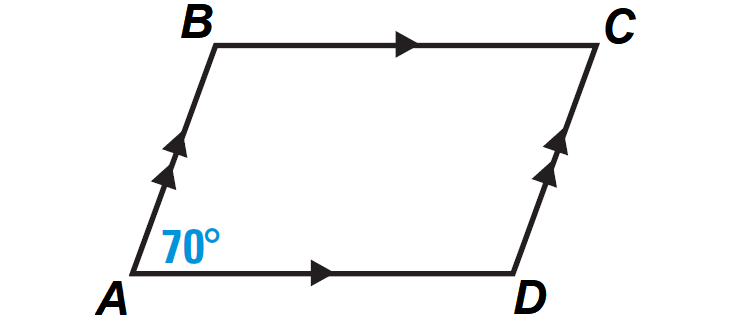
Solution :

Finding the measure of ∠C :

By Theorem, opposite angles of a parallelogram are congruent.

So, we have

m∠C = m∠A

From the diagram, m∠A = 70°.

m∠C = 70°

Finding the measure of ∠B :

By Theorem, consecutive  angles of a parallelogram are supplementary.

So, we have

m∠A + m∠B = 180°

From the diagram, m∠A = 70°.

70° + m∠B = 180°

Subtract 70° from both sides.

 m∠B = 110°

Problem 3 :

Find the value of x in the parallelogram ABCD shown below.

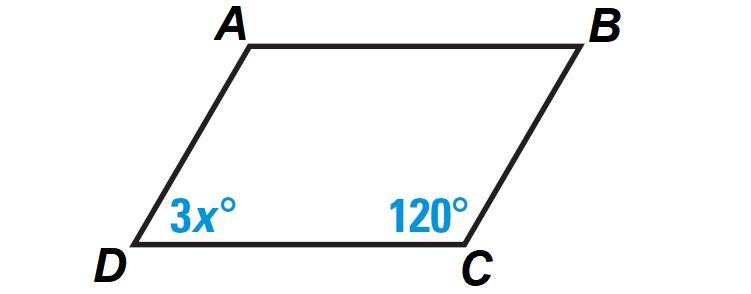
Solution :

By Theorem, consecutive  angles of a parallelogram are supplementary.

So, we have

m∠D + m∠C = 180°

Substitute m∠D = 3x° and m∠C = 120°.

3x° + 120° = 180°

Subtract 120° from both sides.

3x° = 60°

3x = 60

Divide both sides by 3. 

x = 20

Problem 4 :

In the diagram shown below, ABCD and AEFG are parallelograms. Prove that m∠1 ≅ m∠3.

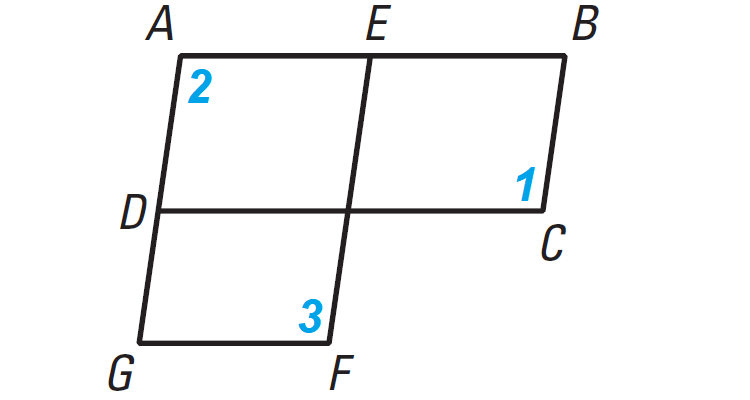
Solution :

Plan : Show that both angles are congruent to m∠2. Then use the Transitive Property of Congruence.

Problem 5 :

In the parallelogram ABCD shown below, prove that WX ≅ YZ and WZ ≅ XY.

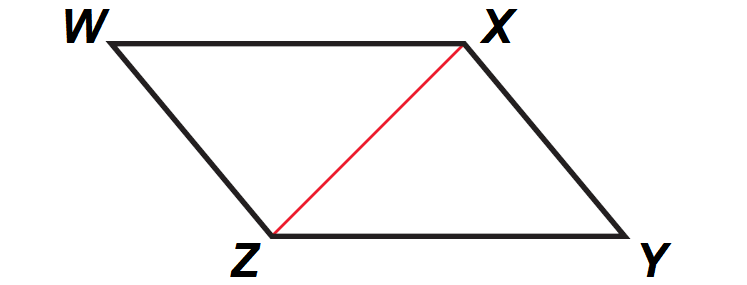
Solution :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.