PROVE THAT THE GIVEN POINTS ARE VERTICES OF RECTANGLE
(i) In a rectangle the length of opposite sides will be equal.
(ii) The rectangle can be divided into two right triangles.
Question 1 :
Examine whether the given points
A(-2, 7), B (5, 4), C (-1, -10) and D (-8, -7)
forms a rectangle.

Solution :
Distance Between Two Points (x1, y1) and (x2 , y2)
√(x2 - x1)2 + (y2 - y1)2
Length of AB :
Here x1 = -2, y1 = 7, x2 = 5 and y2 = 4
= √(5-(-2))2+(4-7)2
= √72+(-3)2
= √(49+9)
= √58 units
Length of BC :
Here x1 = 5, y1 = 4, x2 = -1 and y2 = -10
= √(-1-5)2 + (-10-4)2
= √(-6)2 + (-14)2
= √(36+196)
= √232 units
Length of CD :
Here x1 = -1, y1 = -10, x2 = -8 and y2 = -7
= √(-8-(-1))2 + (-7-(-10))²
= √(-7)2 + 32
= √(49+9)
= √58 units
Length of DA :
Here x1 = -8, y1 = -7, x2 = -2 and y2 = 7
= √(-2-(-8))2 + (7-(-7))2
= √(-2+8)2 + (7+7)2
= √(36+196)
= √232 units
Length of AC :
Here x1 = -2, y1 = 7, x2 = -1 and y2 = -10
= √(-1-(-2))2 + (-10-7)2
= √(-1+2)2 + (-17)2
= √(1+289)
= √290 units
In triangle ABC,
AC2 = AB2 + BC2
√2902 = √582 + √2322
290 = 58 + 232
290 = 290
So, the given points will be the vertices of rectangle.
Question 2 :
Examine whether the given points
P(-3, 0), Q (1, -2) and R (5, 6) and S (1, 8)
forms a rectangle.
Solution :
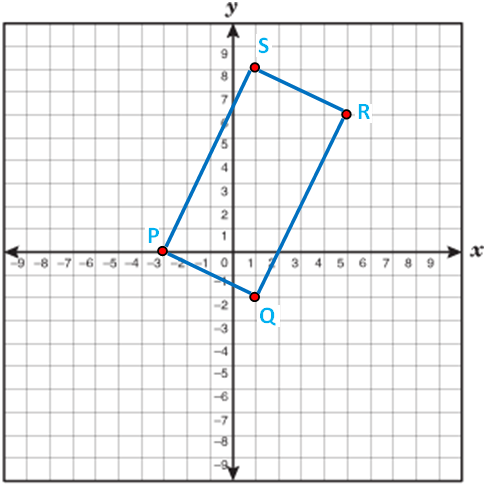
Length of PQ :
Here x1 = -3, y1 = 0, x2 = 1 and y2 = -2
= √(1-(-3))2 + (-2-0)2
= √(1+3)2 + (-2)2
= √42+(-2)²
= √(16+4)
= √20 units
Length of QR :
Here x1 = 1, y1 = -2, x2 = 5 and y2 = 6
= √(5-1)2 + (6-(-2))2
= √42 + (6+2)2
= √(16 + 64)
= √80 units
Length of RS :
Here x1 = 5, y1 = 6, x2 = 1 and y2 = 8
= √(1-5)2+(8-6)2
= √(-4)2+22
= √(16+4)
= √20 units
Length of SP :
Here x1 = 1, y1 = 8, x2 = -3 and y2 = 0
= √(-3-1)2 + (0-8)2
= √(-4)2+(-8)2
= √(16+64)
= √80 units
Length of SP :
Here x1 = 1, y1 = 8, x2 = -3 and y2 = 0
Here x₁ = 1, y₁ = -2, x₂ = 1 and y₂ = 8
= √(1-1)² + (8-(-2))²
= √(0)² + (8+2)²
= √0 + 10²
= √100
= √100 units
In triangle QRS,
QS² = QR² + SR²
(√100)² = (√80) ² + (√20)²
100 = 80 + 20
100 = 100
So the given vertices forms a rectangle.
Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Rational Root Theorem
Feb 06, 25 07:42 PM
Rational Root Theorem or Rational Zero Theorem - Concept - Examples -
How to Find Pythagorean Triplet from One Number
Feb 06, 25 06:10 PM
How to Find Pythagorean Triplet from One Number - Concept - Examples with step by step explanation -
AP Calculus AB Problems with Solutions (Part - 10)
Feb 06, 25 09:46 AM
AP Calculus AB Problems with Solutions (Part - 10)