PROVING QUADRILATERALS ARE RHOMBUSES
We can use the one of the following three ways to prove that quadrilateral is a rhombus.
Way 1 :
We can use the definition and show that the quadrilateral is a parallelogram that has four congruent sides. It is easier, however, to use the Rhombus Corollary and simply show that all four sides of the quadrilateral are congruent.
Way 2 :
Show that the quadrilateral is a parallelogram and that the diagonals are perpendicular.
Way 3 :
Show that the quadrilateral is a parallelogram and that each diagonal bisects a pair of opposite angles.
Example :
Show that the quadrilateral KLMN shown below is a rhombus.
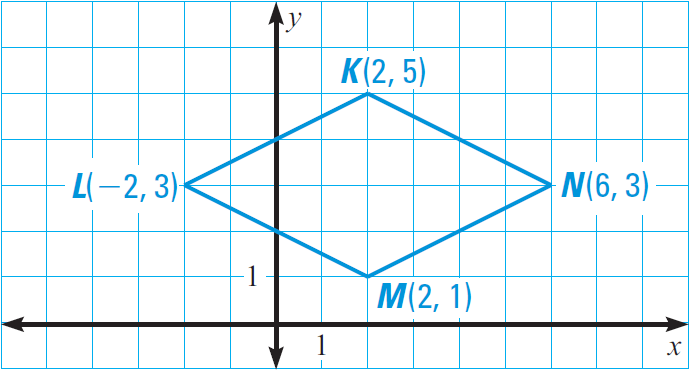
Solution :
We can use any of the three ways described in the concept summary above. For instance, we could show that opposite sides have the same slope and that the diagonals are perpendicular. Another way, shown below, is to prove that all four sides have the same length.
Finding the length of LM :
= √{[(2 - (-2)]2 + (1 - 3)2}
= √{(2 + 2)2 + (- 2)2}
= √{42 + 4}
= √{16 + 4}
= √20
Finding the length of MN :
MN = √{(6 - 2)2 + (3 - 1)2}
= √{42 + 22}
= √{16 + 4}
= √20
Finding the length of NK :
NK = √{(2 - 6)2 + (5 - 3)2}
= √{(-4)2 + 22}
= √{16 + 4}
= √20
Finding the length of KL :
KL = √{(-2 - 2)2 + (3 - 5)2}
= √{(-4)2 + (-2)2}
= √{16 + 4}
= √20
From the above calculations, we have
LM = MN = NK = KL
Hence, KLMN is a rhombus.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus AB Problems with Solutions (Part - 10)
Feb 11, 25 05:37 AM
AP Calculus AB Problems with Solutions (Part - 10) -
AP Calculus AB Problems with Solutions (Part - 9)
Feb 10, 25 06:02 PM
AP Calculus AB Problems with Solutions (Part - 9) -
Digital SAT Math Problems and Solutions (Part - 108)
Feb 10, 25 07:03 AM
Digital SAT Math Problems and Solutions (Part - 108)