PUT RATIONAL NUMBERS IN ORDER WORKSHEET

Problem 1 :

Write the following rational numbers in order from greatest to least.

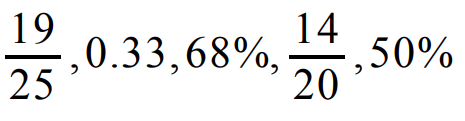
Problem 2 :

Write the following rational numbers in order from greatest to least.

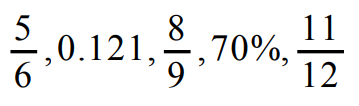
Problem 3 :

Write the following rational numbers in order from least to greatest.

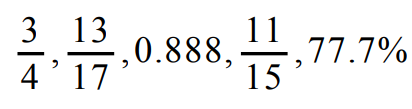
Solutions

Problem 1 :

Write the following rational numbers in order from greatest to least.

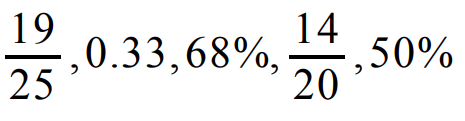
19/25 is already a fraction, so we can leave it as it is.	= 19/25
For converting the second number 0.33 into fraction, we have to multiply both numerator and denominator by 100.	0.33 x (100/100) = 33/100
68% can be written as 68/100	= 68/100
Since 14/20 is already in fractional form, we don't have to convert this	14/20
50% can be written as 50/100	50/100

The denominators of the above fractions are 25, 100, 100, 20 and 100.

Since the denominators are different, we have to find least common multiple.

L.C.M = 100

19/25 (1) ==> (19/25) x (4/4) = 76/100

0.33 (2) ==> (33/100)

68% (3) ==> (68/100)

14/20 (4) ==> (14/20) x (5/5) = 70/100

50% (5) ==> (50/100)

The rational numbers from greatest to least is 76/100, 70/100, 68/100, 50/100, 33/100

Hence the required order is 19/25, 14/20, 68%, 50%, 0.33

Problem 2 :

Write the following rational numbers in order from greatest to least.

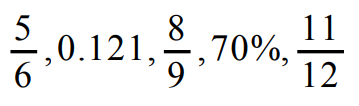
5/6 is already a fraction, so we can leave it as it is.	= 5/6
For converting the second number 0.121 into fraction, we have to multiply both numerator and denominator by 1000.	0.121 x (1000/1000) = 121/1000
8/9 is already a fraction, so we can leave it as it is.	= 8/9
70% can be written as 70/100	70/100
11/12 is already a fraction, so we can leave it as it is.	11/12

The denominators of the above fractions are 6, 1000, 9, 100 and 12.

Since the denominators are different, we have to find least common multiple.

L.C.M = 3 x 2 x 5 x 2 x 5 x 10 x 3 = 9000

5/6 (1)==> (5/6) x (1500/1500) = 7500/9000 (3)

0.121 (2)==> 0.121 x (1000/1000) = 121/1000 (5)

8/9 (3)==> (8/9) (1000/1000) = 8000/9000 (2)

70% (4)==> (70/100) x (90/90) = 6300/9000 (4)

11/12 (5)==> (11/12) x (750/750) = 8250/9000 (1)

The rational numbers from greatest to least is 8250/9000, 8000/9000, 7500/9000, 6300/9000, 121/9000

Hence the required order is 11/12, 8/9, 5/6, 70%, 0.121

Problem 3 :

Write the following rational numbers in order from least to greatest.

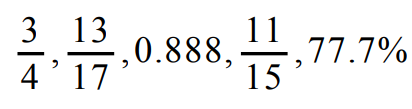
3/4 is already a fraction, so we can leave it as it is.	= 3/4
13/17 is already a fraction, so we can leave it as it is.	= 13/17
To convert 0.888 as fraction, we have to multiply both numerator and denominator by 1000	0.888 x (1000/1000) = 888/1000
11/15 is already a fraction, so we can leave it as it is.	11/15
77.7% can be written as 77.7/100. In order to convert this into fraction, we have to multiply both numerator and denominator by 10.	(77.7/100) x (10/10) = 777/1000

The denominators of the above fractions are 4, 17, 1000, 15 and 1000.

Since the denominators are different, we have to find least common multiple.

L.C.M = 5 x 2 x 2 x 5 x 17 x 10 x 3 x 10 = 510000

3/4 (1)==>(3/4)x(127500/127500) = 382500/510000 (3)

13/17 (2)==>(13/17)x(30000/30000)=390000/510000 (4)

0.888(3)==>

(8/1000)x(510/510)=4080/510000 (1)

11/15 (4)==>

(11/15)x(34000/34000)=374000/510000 (2)

77.7 (5)==>

(777/1000) x (510/510) = 396270/510000 (5)

The rational numbers from greatest to least is 8250/9000, 8000/9000, 7500/9000, 6300/9000, 121/9000

Hence the required order is 0.888, 11/15, 3/4, 13/17, 77.7%

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

PUT RATIONAL NUMBERS IN ORDER WORKSHEET

Solutions

Recent Articles

SAT Math Video Solutions (Part - 1)

Divisibility Rules 1 to 10

Trigonometric Identities Worksheet