QUESTION OF FINDING CENTROID OF TRIANGLE
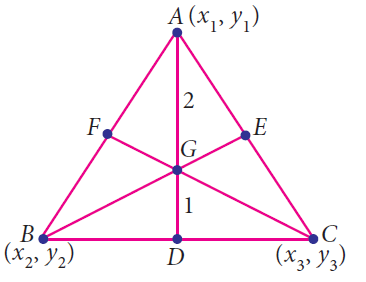
The centroid G of the triangle with vertices A(x1, y1), B(x2, y2) and C(x3, y3) is
G [ (x1 + x2 + x3)/3, (y1 + y2 + y3)/3 ]
Practice Questions
Question 1 :
Th e vertices of a triangle are (1, 2), (h, −3) and (−4, k). If the centroid of the triangle is at the point (5, −1) then find the value of √(h + k)2 + (h + 3k)2.
Solution :
Let A (1, 2) B (h, −3) and C (−4, k) be the vertices of the triangle.
Centroid of the triangle = (5, -1)
G [ (x1 + x2 + x3)/3, (y1 + y2 + y3)/3 ] = (5, -1)
(1 + h - 4)/3, (2 - 3 + k)/3 = (5, -1)
(h - 3)/3, (-1 + k)/3 = (5, -1)
|
(h - 3)/3 = 5 h - 3 = 15 h = 15 + 3 h = 18 |
(-1 + k)/3 = -1 -1 + k = -3 k = -3 + 1 k = -2 |
√(h + k)2 + (h + 3k)2 = √(18 - 2)2 + (18 - 6)2
= √162 + 122
= √256 + 144
= √400
= 20
Question 2 :
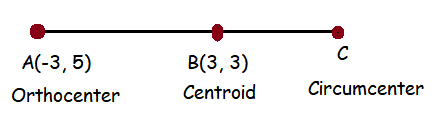
Orthocentre and centroid of a triangle are A(−3, 5) and B(3, 3) respectively. If C is the circumcentre and AC is the diameter of this circle, then find the radius of the circle.
Solution :
The distance between the centroid and the orthocenter is twice the distance between the centroid and he circumcenter. The centroid is dividing the othocenter and circumcenter in the ratio 2 : 1.
= (mx2 + nx1)/(m + n), (my2 + ny1)/(m + n)
Let C be (a, b)
(2a+1(-3))/(2+1), (2b+1(5))/(2+1) = (3, 3)
(2a-3)/3, (2b+5)/3 = (3, 3)
Equating the x and y coordinates, we get
|
(2a - 3)/3 = 3 2a - 3 = 9 2a = 9 + 3 2a = 12 a = 6 |
(2b+5)/3 = 3 2b + 5 = 9 2b = 9 - 5 2b = 4 b = 4/2 = 2 |
Hence the circumcenter is (6, 2)
AC = diameter of the circle
A(-3, 5) C(6, 2)
= √(6+3)2 + (2-5)2
= √92 + (-3)2
= √(81+9)
= √90
= 3√10
Radius = 3√10/2 = 3√(5/2)
Question 3 :
ABC is a triangle whose vertices are A(3, 4), B(−2, −1) and C(5, 3) . If G is the centroid and BDCG is a parallelogram then find the coordinates of the vertex D.
Solution :
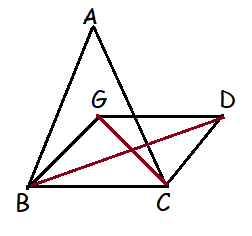
So, midpoint of diagonal BD = midpoint of diagonal CG
let D = (a, b)
midpoint of BD = [(-2+a)/2, (-1+b)/2 ]
midpoint of CG = [(5+2)/2,(3 + 2)/2 ] = (7/2, 5/2)
hence, [(-2+x)/2, (-1+y)/2] = (7/2, 5/2)
(-2+a)/2 = 7/2 => a = 9
(-1+b)/2 = 5/2 => b = 6
So the required vertex is D (9,6)
Question 4 :
If (3/2, 5) (7, -9/2) and (13/2, -13/2) are mid-points of the sides of a triangle, then find the centroid of the triangle.
Solution :
Let the given midpoints be (x1, y1) (x2, y2) and (x3, y3)
A (x1 + x3 - x2, y1 + y3 - y2)
B (x1 + x2 - x3, y1 + y2 - y3)
C (x2 + x3 - x1, y2 + y3 - y1)

Centroid = (1 + 2 + 12)/3 , (3 + 7 - 16)/3
= (15/3), (-6/3)
= (5, -2)
Hence the required centroid is (5, -2).
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 199)
Jul 02, 25 07:06 AM
Digital SAT Math Problems and Solutions (Part - 199) -
Logarithm Questions and Answers Class 11
Jul 01, 25 10:27 AM
Logarithm Questions and Answers Class 11 -
Digital SAT Math Problems and Solutions (Part -198)
Jul 01, 25 07:31 AM
Digital SAT Math Problems and Solutions (Part -198)