REFLECTIONS

Using Reflections in a Plane

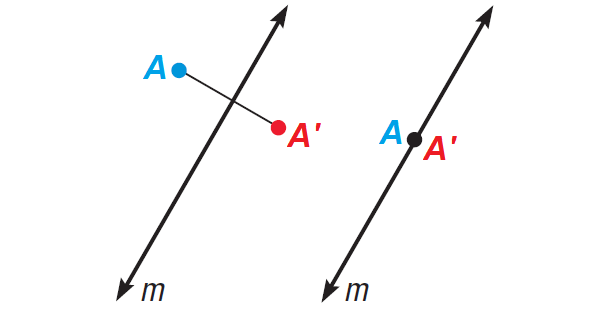
One type of transformations uses a line that acts like a mirror, with an image reflected in the line. This transformation is a reflection and the mirror line is the line of reflection.

A reflection in a line m is a transformation that maps every point A in the plane to a point A', so that the following properties are true.

1. If A is not on m, then m is the perpendicular bisector of AA'.

2. If A is on m, then A = A'.

Reflections in a Coordinate Plane

Example 1 :

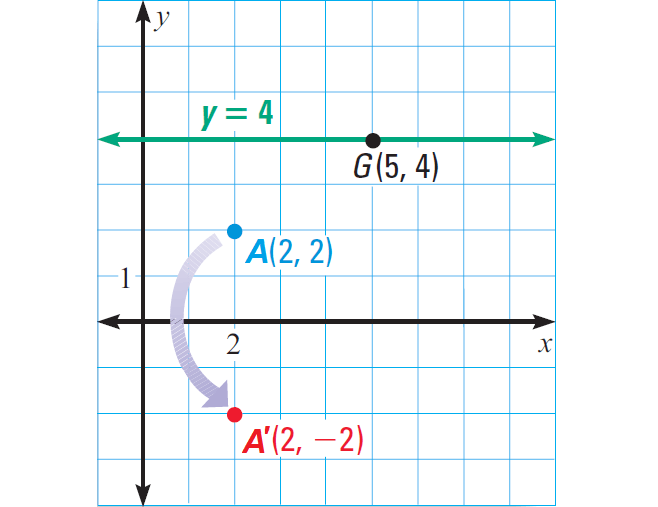
Graph the given reflections.

a. A(2, 2) in the x-axis.

b. G(5, 4) in the line y = 4.

Solution (a) :

Because A is two units above the x-axis, its reflection, A' is two units below the x-axis.

Solution (b) :

Start by graphing y = 4 and G. From the graph, we can see that G is on the line. This implies G = G'.

Reflections in the Coordinate Axes

Reflections in the coordinate axes have the following properties.

1. If (x, y) is reflected in the x-axis, its image is the point :

(x, -y)

2.  If (x, y) is reflected in the y-axis, its image is the point :

(-x, y)

Reflection Theorem

A reflection is an isometry.

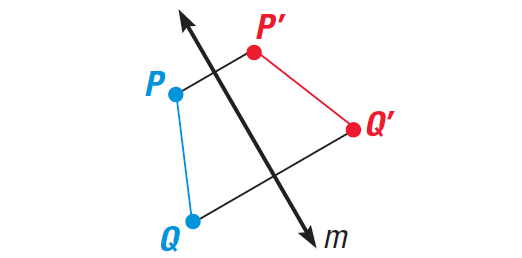
To prove the Reflection Theorem, we have to show that a reflection preserves the length of a segment. Consider a segment PQ that is reflected in a line m to produce P'Q'. The four cases to consider are shown below.

Case 1 :

P and Q are on the same side of m.

It has been illustrated in the diagram shown below.

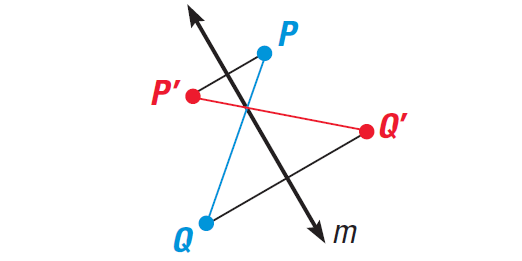
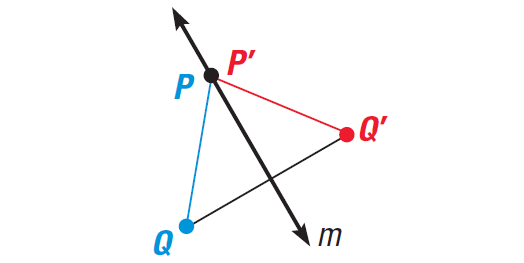
Case 2 :

P and Q are on opposite sides of m.

It has been illustrated in the diagram shown below.

Case 3 :

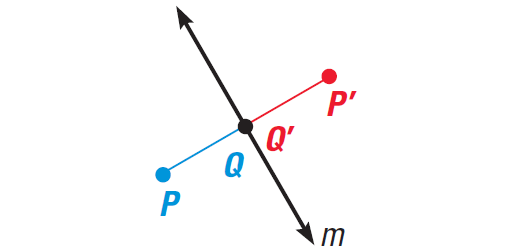
One point lies on m and PQ is not perpendicular to m.

It has been illustrated in the diagram shown below.

Case 4 :

Q lies on m and PQ ⊥ m.

It has been illustrated in the diagram shown below.

Proof of Case 1 of Reflection Theorem 

Given : A reflection in m maps P onto P' and Q onto Q'.

Prove : PQ = P'Q'

Proof :

For this case, P and Q are on the same side of line m.

Draw PP' and QQ', intersecting line m at R and S.

Draw RQ and RQ'.

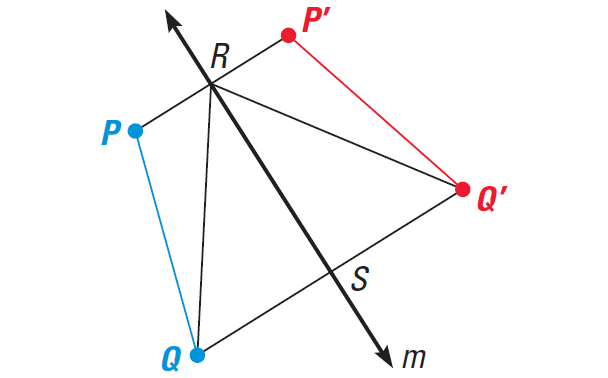
By the definition of a reflection,

m ⊥ QQ' and QS ≅ Q'S

It follows that ΔRSQ ≅ ΔRSQ' using SAS Congruence Postulate.

This implies

RQ ≅ RQ' and ∠QRS ≅ ∠Q'RS

Because RS is a perpendicular bisector of PP', we have enough information to apply SAS to conclude that

ΔRQP ≅ ΔRQ'P

Because corresponding parts of congruent triangles are congruent,

PQ = P'Q'

Reflections and Line Symmetry

A figure in the plane has a line of symmetry, if the figure can be mapped onto itself by a reflection in the line.

Finding Lines of Symmetry

Example 2 :

Hexagons can have different lines of symmetry depending on their shape.

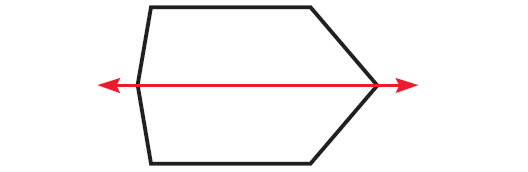
Case 1 :

The hexagon shown below has only one line of symmetry.

Case 2 :

The hexagon shown below has only one line of symmetry.

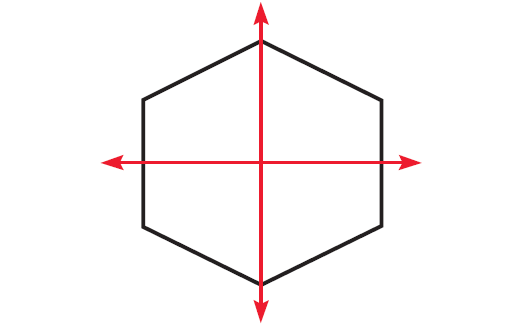
Case 3 :

The hexagon shown below has only one line of symmetry.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.