ROLLES THEOREM PRACTICE PROBLEMS WITH ANSWERS

Verify Rolle's theorem for the following functions:

(1) f (x) = sin x   0 ≤ x ≤ π

(2) f (x) = x², 0 ≤ x ≤ 1

(3) f (x) = |x - 1|, 0 ≤ x ≤ 2

(4) f (x) = 4 x³ - 9 x, -3/2 ≤ x ≤ 3/2

(5) Using Rolle's theorem find the points on the curve'

y  =  x² + 1,

- 2 ≤ x ≤ 2 where the tangent is parallel to x - axis.

(6)  The table below gives selected values of a function 𝑓. The function is twice differentiable with f''(x) > 0

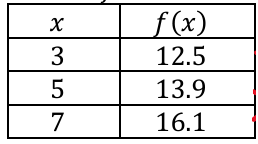
Which of the following could be the value of f'(5) ?

a)  0.5      b)  0.7      c)  0.9     d)  1.1

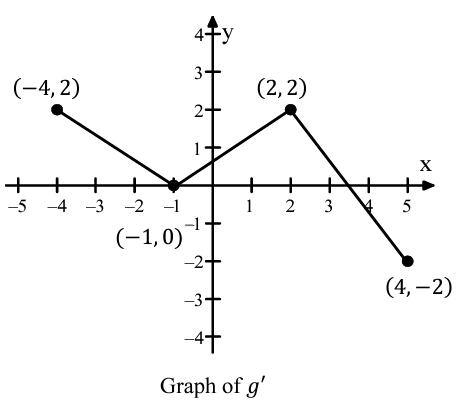
(7)  Let 𝑔 be a continuous function. The graph of the piecewise-linear function g', the derivative of g is shown above for -4 ≤ x ≤ 4. Does the mean value theorem applied on the interval -4 ≤ x ≤ 4 guarantee the value of c, for -4 < x < 4, such that g''(c) is equal to this average rate of change ? why or why not ?

Problem 1 :

f(x)  =  sin x,   0 ≤ x ≤ π

Solution :

If f(x) be a real valued function that satisfies the following three conditions.

(1)  f(x) is defined and continuous on [0, π] 

(2)  f(x) is differentiable on the open interval (0, π).

f(x)  =  sin x

f(0)  =  sin 0  ==>  0

f(π)  =  sin π  ==> 0

f(0)  =  f(π)

from this we come to know that the given function satisfies all the conditions of Rolle's theorem. c ∈ (0,π) we can find the value of c by using the condition f '(c) = 0.

f(x)  =  sin x

f'(x)  =  cos x

f'(c)  =  cos c

f'(c)  =  0

cos c  =  0

c  =  (2n+1) (π/2)

       c  =  π/2,3π/2,5π/2,.............

Here π/2 is the only value that is in the given interval. So, the value of c = π/2.

Problem 2 :

f(x)  =  x², 0 ≤ x ≤ 1

Solution :

If f(x) be a real valued function that satisfies the following three conditions.

(1)  f(x) is defined and continuous on [0, 1] 

(2)  f(x) is differentiable on the open interval (0, 1).

f(x)  =  x²

f(0)  =  0²  ==>  0

f(1)  =  1²  ==>  1

f(0)  ≠  f(1)

The given function is not satisfying all the conditions of mean value theorem. So, we cannot find the value of c.

Problem 3 :

f(x)  =  |x-1|, 0 ≤ x ≤ 2

Solution :

If f(x) be a real valued function that satisfies the following three conditions.

1) f(x) is defined and continuous on [0, 2] 

2) f(x) is not differentiable on (0, 2).

Since the given function is not satisfying all the conditions Rolle's theorem is not admissible.

Problem 4 :

f(x) = 4 x³-9x, -3/2 ≤ x ≤ 3/2

Solution :

If f(x) be a real valued function that satisfies the following three conditions.

(1)  f(x) is defined and continuous on [-3/2, 3/2] 

2) f(x) is not differentiable on (-3/2,3/2)

f(x) = 4x³-9 x

f(-3/2)  =  f(3/2)

c ∈ (-3/2, 3/2) we can find the value of c by using the condition f'(c)  =  0.

f(x)  =  4x³-9x

f'(x)  =  12x²- 9(1)

=  12x²-9

f'(c)  =  12c²-9

f'(c)  =  0

12c²-9  =  0

12c²  =  9

c²  =  9/12

c  =  ± √3/2

Problem 5 :

y = x² + 1    - 2 ≤ x ≤ 2 

Solution :

If f(x) be a real valued function that satisfies the following three conditions.

1) f(x) is defined and continuous on [-2,2] 

2) f(x) is not differentiable on the open interval (-2,2).

y  =  x² + 1

from this we come to know that the given function satisfies all the conditions of Rolle's theorem.

c ∈ (-2,2). We can find the value of c by using the condition f'(c)  =  0.

f(x)  =  x² + 1

f'(x)  =  2x

f'(c)  =  2 c

f'(c)  =  0

2c  =  0  

c  =  0

f(0)  =  0²+1

= 1

Therefore the required point on the curve is (0, 1).

Problem 6 :

The table below gives selected values of a function 𝑓. The function is twice differentiable with f''(x) > 0

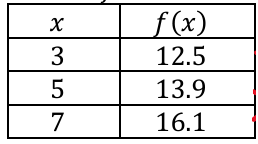
Which of the following could be the value of f'(5) ?

a)  0.5      b)  0.7      c)  0.9     d)  1.1

Solution :

= [f(5) - f(3)] / (5 - 3)

= (13.9 - 12.5)/2

= 1.4/2

= 0.7

= [f(7) - f(5)] / (7 - 5)

= (16.1 - 13.9)/2

= 2.2/2

= 1.1

The required values should be in between 0.7 and 1.1

So, the answer is 0.9 (option c).

Problem 7 :

Let 𝑔 be a continuous function. The graph of the piecewise-linear function g', the derivative of g is shown above for -4 ≤ x ≤ 4. Does the mean value theorem applied on the interval -4 ≤ x ≤ 4 guarantee the value of c, for -4 < x < 4, such that g''(c) is equal to this average rate of change ? why or why not ?

Solution :

Average rate of change = [g'(4) - g'(-4)] / (4 - (-4))

From the graph of g', we get two points (4, -2) and (-4, 2)

= (-2 - 2) / (4 + 4)

= -4/8

= -1/2

No, because 𝒈′𝒙 is not differentiable. It has several corners. The MVT only applies if the function is differentiable.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.