ROUNDING DECIMALS

Example 1 :

Round 12.358 to the nearest tenth.

Solution :

Underline 3, the digit in the tenths place.

12.358

The digit to the right of the underlined digit is 5, round up.

Therefore, 12.358 rounded to the nearest tenths  place is 12.4.

Example 2 :

Round 56.358345 to the nearest thousandth.

Solution :

Underline 8, the digit in the thousandths place.

56.358345

The digit to the right of the underlined digit is less than 5, keep the underlined digit as it is.

Therefore, 56.358345 rounded to the nearest thousandths place is 56.358.

Example 3 :

Round 3.457 to two decimal places.

Solution :

Underline 5, the digit in the second decimal place.

3.457

The digit to the right of the underlined digit is more than 5, round up.

Therefore, 3.457 rounded to two decimal places is 3.46.

Example 4 :

Round 6.78301 to three decimal places.

Solution :

Underline 3, the digit in the third decimal place.

6.78301

The digit to the right of the underlined digit is less than 5, keep the underlined digit as it is.

Therefore, 6.78301 rounded to three decimal places is 6.783.

Example 5 :

Round 52.348 to the nearest

a) integer and b) hundredth.

Solution :

Part (a) :

Underline 2, the digit in the ones place. 52.348

The digit to the right of the underlined digit is less than 5, keep the underlined digit as it is and drop all the digits after the decimals point.

Therefore, 52.348 rounded to the nearest integer is 52.

Part (b) :

Underline 4, the digit in the hundredths place. 52.348

The digit to the right of the underlined digit is more than 5, round up.

Therefore, 52.348 rounded to the nearest hundredths place is 52.35.

Example 6 :

Round the following number to the nearest tenth.

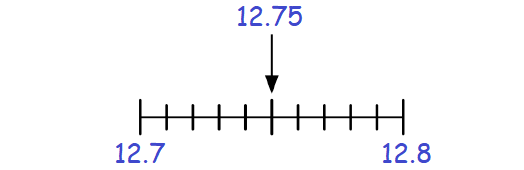
Solution :

In 12.75, the digit at tenths place is 7.

The digit to the right of 7 is 5.

Then, add 1 to the digit 7 at tenths place and drop the digit 5 to the right of 7.

Therefore, 12.75 rounded to the nearest tenth is 12.8.

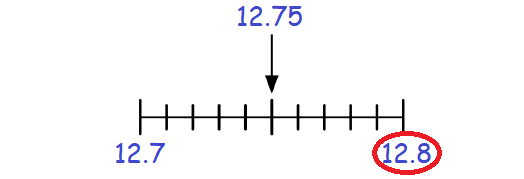
Example 7 :

Round the following number to the nearest tenth.

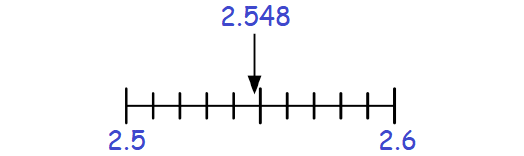
Solution :

In 2.548, the digit at tenths place is 5.

The digit to the right of 5 is 4, which is less than 5.

Then, keep the digit 5 at tenths place as it is and drop all the digits to the right of 5.

Therefore, 2.548 rounded to the nearest tenths is 2.5.

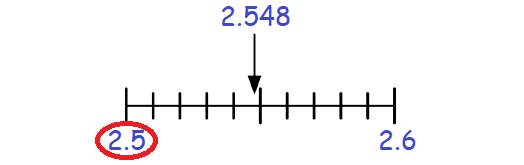
Example 8 :

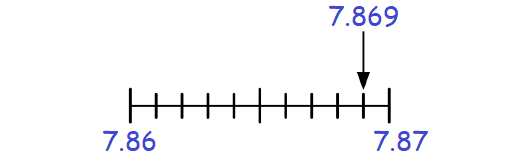
Round the following number to the nearest hundredth.

Solution :

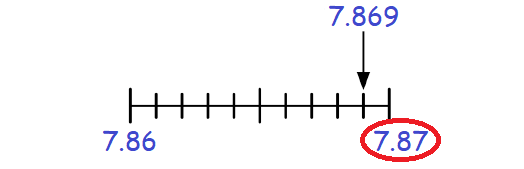
In 7.869, the digit at hundredths place is 6.

The digit to the right of 6 is 9, which is greater than 5.

Then, add 1 to the digit 6 at hundredths place and drop the digit 9 to the right of 6.

Therefore, 7.869 rounded to the nearest hundredth is 7.87.

Example 9 :

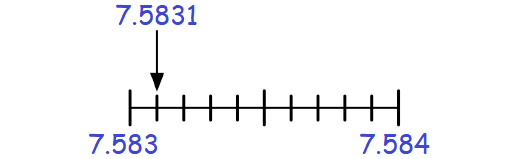
Round the following number to the nearest thousandth.

Solution :

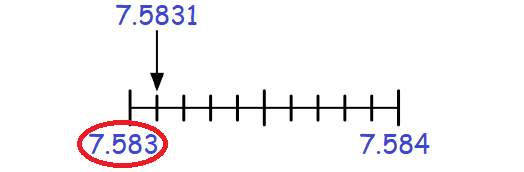
In 7.5831, the digit at thousandths place is 3.

The digit to the right of 3 is 1, which is less than 5.

Then, keep the digit 3 at thousandths place as it is and drop the digit 1 to the right of 3.

Therefore, 7.5831 rounded to the nearest thousandths is 7.583.

Example 10 :

Round the following number to the nearest ten thousandth.

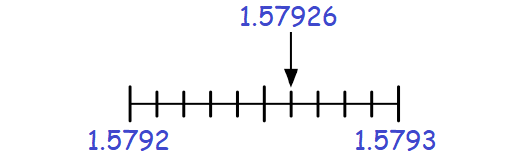
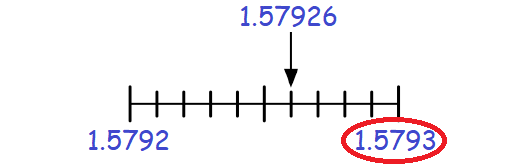
Solution :

In 1.57926, the digit at ten thousandths place is 2.

The digit to the right of 2 is 6, which is greater than 5.

Then, add 1 to the digit 2 at ten thousandths place and drop the digit 6 to the right of 2.

Therefore, 1.57926 rounded to the nearest ten thousandths is 1.5793.

Example 11 :

Find the circumference of the circle whose radius is 9 cm. Use π ≈ 3.14 and round your answer to the nearest tenth.

Solution :

Formula for circumference of a circle :

= 2πr

Substitute π ≈ 3.14 and r = 7.

≈ 2(3.14)(9)

= 56.52

The digit to the right of the underlined digit is less than 5, keep the underlined digit as it is.

= 56.5 cm

Therefore, the circumference of the circle is about 56.5 cm.

Example 12 :

Find the area of the circle whose radius is 12 cm. Use π ≈ 3.14 and round your answer to the nearest whole number.

Solution :

Formula for area of a circle :

= πr²

Substitute π ≈ 3.14 and r = 7.

≈ (3.14)(12)²

= 452.16

The digit to the right of the underlined digit is less than 5, keep the underlined digit as it is.

= 452 cm²

Therefore, the area of the circle is about 452 cm².

Example 13 :

In a school of 2487 students, about 85% of the students are using mobile phones. Approximately how many students are using mobile phone?

Solution :

Number of students who are using mobile phone :

= 0.85 x 2487

= 2113.95

Number of students is always a whole number.

So, round 2113.95 to the nearest whole number.

= 2113.95

The digit to the right of the underlined digit is more than 5, round up.

= 2114

Out of 2487 students in the school, approximately 2114 students are using mobile phones.

Example 14 :

James writes down two numbers, A and B. A and B have 2 decimal places. James rounds A to the nearest tenth and calls his answer C. He rounds B to the nearest tenth and calls his answer D. James says the difference between A and B cannot be the same as the difference between C and D. Show that he is incorrect.

Answer :

Let A = 2.22 and B = 1.12.

Then the difference is

= 2.22 - 1.12

= 1.1

Given : James rounds A to the nearest tenth and calls his answer C. He rounds B to the nearest tenth and calls his answer D.

Then, C = 2.2 and D = 1.1.

The difference is

= 2.2 - 1.1

= 1.1

The difference between A and B and the difference between C and D are are same.

But, James says the difference between A and B cannot be the same as the difference between C and D.

So, James is incorrect.

Example 15 :

Jessica has rounded a number to the nearest thousandth. Her answer is 9.537. Write down 10 different possible numbers that she could have rounded.

Answer :

9.5365

9.5366

9.5367

9.5368

9.5369

9.5370

9.5371

9.5372

9.5373

9.5374

Practice Questions

Click here to get detailed answers for the above questions.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.