SAT MATH QUESTIONS AND ANSWERS - 2
(NO CALCULATOR)

Question 1 :

A certain job can be done in 20 hours by 4 people. How many people are needed to do the same job in 10 hours?

(A)  2

(B)  4

(C)  8

(D)  10

Answer :

The job can be done by 4 people in 20 hours.

But, the job has to be completed in 10 hours.

When the number of hours is decreased, the number of people has to be increased.

When one quantity decreases, the other quantity increases. This is inverse proportion.

Let y be the number of people and x be the number hours.

Since x and y are in inverse proportion, the equation which relates x and y is

y = ᵏ⁄ₓ

Use the given information and solve for k.

Substitute x = 20 and y = 4.

4 = ᵏ⁄₂₀

k = 80

Then the equation is

y = ⁸⁰⁄ₓ

Substitute x = 10.

y = ⁸⁰⁄₁₀

y = 8

8 people are needed to complete the job in 10 hours.

Therefore, the correct answer choice is (C).

Question 2 :

Which of the following is equivalent to f(x) = x² - 6x + 7?

(A)  f(x) = (x + 3)² + 5

(B)  f(x) = (x - 3)² + 2

(C)  f(x) = (x - 3)² - 2

(D)  f(x) = (x - 7)(x + 1)

Answer :

f(x) = x² - 6x + 7

In the quadratic function above, x² - 6x + 7 is not factorable and it can not be written in factored form as given in option (D).

Write the given quadratic function in vertex form.

f(x) = x² - 6x + 7

f(x) = x² - + 3² - 3² + 7

f(x) = (x - 3)² - 3² + 7

f(x) = (x - 3)² - 9 + 7

f(x) = (x - 3)² - 2

Therefore, the correct answer choice is (C).

Question 3 :

If 24x² - kx + 16 = (3x + 4)(ax - b) for all values of x, where a, b and k are constants, what is the value of k?

(A)  -44

(B)  -12

(C)  12

(D)  44

Answer :

24x² - kx + 16 = (3x + 4)(ax - b)

24x² - kx + 16 = 3ax² - 3bx + 4ax - 4b

24x² - kx + 16 = 3ax² + 4ax - 3bx - 4b

24x² - kx + 16 = 3ax² + (4a - 3b)x - 4b

Comparing the coefficients of like terms,

Substitute a = 8 and b = -4 into 'k = 3b - 4a'.

k = 3(-4) - 4(8)

k = -12 - 32

k = -44

Therefore, the correct answer choice is (A).

Question 4 :

In the xy-plane, the equation of line ℓ is x + 3y = 5. If line m is perpendicular to line ℓ, what is a possible equation of line m?

(A)  y = -(⅓)x + 2

(B)  y = (⅓)x - 1

(C)  y = -3x + 1

(D)  y = 3x + ⅔

Answer :

Write the equation of line ℓ in slope-intercept form.

x + 3y = 5

3y = -x + 5

y = ⁽⁻ˣ ⁺ ⁵⁾⁄₃

y = -ˣ⁄₃ + ⁵⁄₃

y = (-⅓)x + ⁵⁄₃

The slope of the line ℓ is -⅓.

Since the line ℓ is perpendiculat to line m, the slope of the line m :

= 3

Among the given answer choices, the equation in (D) has a slope 3. So, the equation in (D) is a possible equation of line m.

Therefore, the correct answer choice is (D).

Question 5 :

(A)  3

(B)  4

(C)  5

(D)  6

Answer :

3^{3a - b} = 3⁴

Since two terms are equal with same base, the exponents can be equated.

3a - b = 4 ----(1)

Given :

a + b = 8 ----(2)

Add (1) and (2) :

4a = 12

a = 3

Therefore, the correct answer choice is (A).

Question 6 :

In a right triangle, one of the angles is x°. If tanx° = ⁵⁄₁₂, what is the value of sinx°?

Answer :

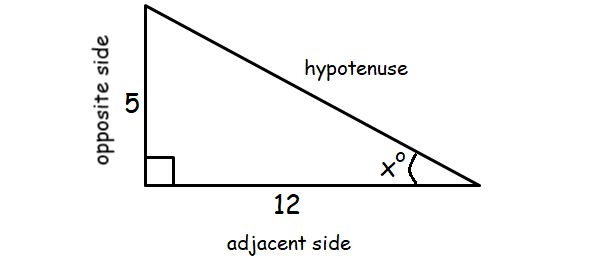
Using Pythagorean Theorem, the length of hypotenuse :

= √169

= 13

Question 7 :

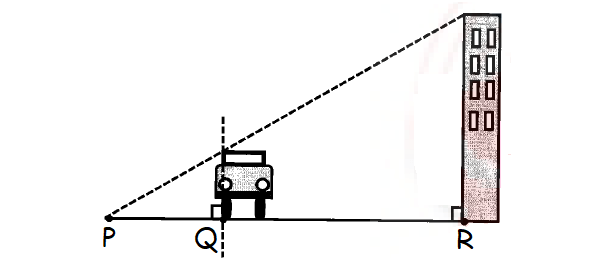
Dawson needs to measure the height of a building near his house. He chooses a point P on the ground where he can visually align the roof of his car with the edge of the building roof. The height of the car is 4 feet and the distance from point P to Q is 10 feet, as shown in the figure above. If the distance from point Q to point R is 80 feet, and the height of the building is k feet, what is the value of k?

Answer :

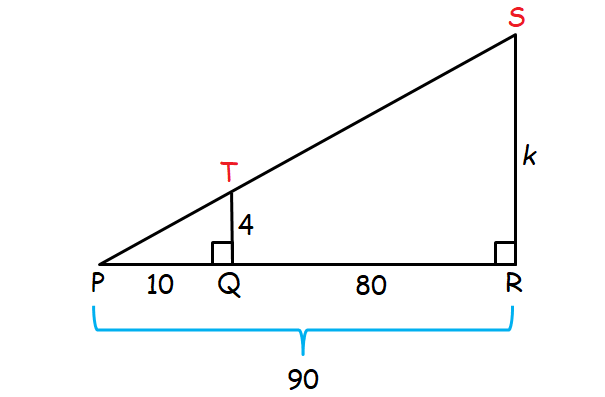
In the figure above, consider the two triangles PRS and PQT.

m∠P = m∠P (common angle)

m∠R = m∠S (right angle)

By Angle-Angle similarity postulate, two triangle PRS and PQT are similar.

ΔPRS ∼ ΔPQT

So, the corresponding sides are proportional.

k = 36

Question 8 :

If a(x + 1) + b(x - 1) = 7x for all real number x, where a and b are constants, what is the value a?

Answer :

a(x + 1) + b(x - 1) = 7x

ax + a + bx - b = 7x

ax + bx + a - b = 7x

(a + b)x + (a - b) = 7x + 0

Comparing the coefficients of like terms,

a + b = 7 ----(1)

a - b = 0 ----(2)

Adding (1) and (2),

2a = 7

a = 3.5

Question 9 :

According to the formula p = (⁴⁄₃)k + 81, if the value of p is increased by 16, by how much does the value of k increase?

Answer :

When p is increased 16, let k be increased by a.

p = (⁴⁄₃)k + 81

p + 16 = (⁴⁄₃)(k + a) + 81

p + 16 = (⁴⁄₃)k + (⁴⁄₃)a + 81

Substitute p = (⁴⁄₃)k + 81.

(⁴⁄₃)k + 81 + 16 = (⁴⁄₃)k + (⁴⁄₃)a + 81

Subtract (⁴⁄₃)k + 81 on both sides.

16 = (⁴⁄₃)a

a = 12

When p is increased by 16, the value of k has to be increased by 12.

Question 10 :

x² + y² = 56

y = √x

According to the system of equations above, what is the value of x?

Answer :

x² + y² = 56 ----(1)

y = √x ----> y² = x

Substitute y² = x into (1).

x² + x = 56

x² + x - 56 = 0

x² - 7x + 8x - 56 = 0

x(x - 7) + 8(x - 7) = 0

(x - 7)(x + 8) = 0

x - 7 = 0  or  x + 8 = 0

x = 7  or  x = -8

When x = -8, we get y = √-8, which is imaginary.

x = -8 can not be accepted.

Therefore,

x = 7

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.