SHIFTING GRAPH UP AND DOWN EXAMPLES

About "Shifting Graph Up and Down Examples"

Shifting Graph Up and Down Examples :

Here we are going to see some examples to learn how to shift the graph up or down.

Shifting Graph Up and Down Examples

Question 1 :

Define a function g by

g(x) = f(x) + 1,

where f is the function defined by f(x) = x², with the domain of f the interval [−1, 1].

(a) Find the domain of g.

(b) Find the range of g.

(c) Sketch the graph of g.

Solution :

(a)  Here g(x) is defined precisely defined by f(x). In  other words, the domain of g equals the domain of f. Thus the domain of g is the interval [−1, 1].

(b)  To find the range of g, we have to apply the values that we find the domain of g. 

By adding every number with the of f, we may find the range of g.

f(x) = x²

If x = -1, then y = 1

If x = 0, then y = 0

If x = 1, then y = 1 

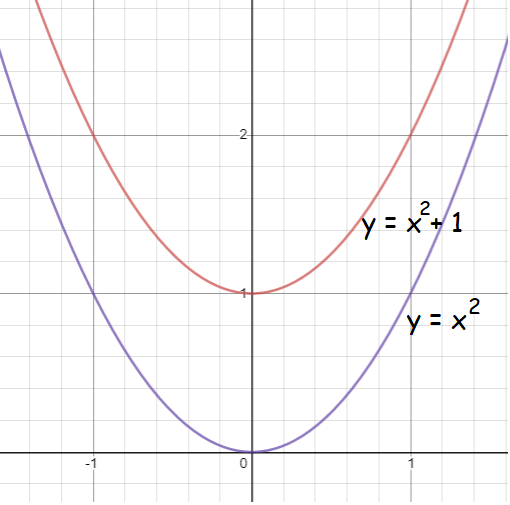
Range of f is [0, 1]. By adding 1 to every values, we get the range of the function g(x) is [1, 2].

(c)  g(x)  =  x² + 1

Here 1 is added with the function, so we have to move the graph of the function 1 unit up. 

Question 2 :

Define a function h by h(x) = f(x) − 1, where f is the function defined by f(x) = x², with the domain of f the interval [−1, 1].

(a) Find the domain of h.

(b) Find the range of h.

(c) Sketch the graph of h.

Solution :

(a)  Here h(x) is defined precisely defined by f(x). In  other words, the domain of f equals the domain of f. Thus the domain of h is the interval [−1, 1].

(b)  To find the range of h, we have to apply the values that we find the domain of f. 

f(x) = x²

If x = -1, then y = 1

If x = 0, then y = 0

If x = 1, then y = 1 

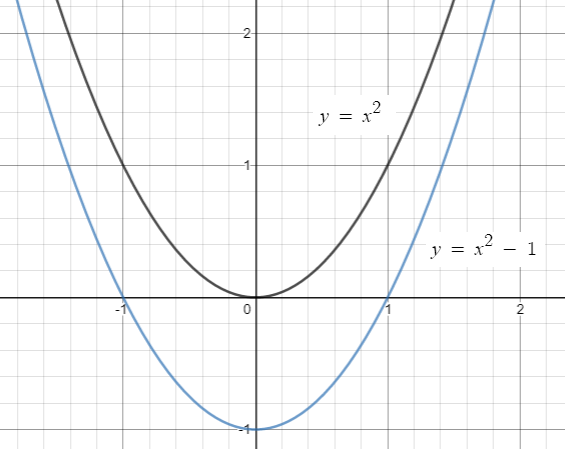
Then range of the function h(x) is [0, 1].By subtracting 1 from every values, we get the range of the function h(x) that is [-1, 0].

(c)  h(x)  =  x² - 1

Here 1 is subtracted  from the function, so we have to move the graph of the function 1 unit . 

Question 3 :

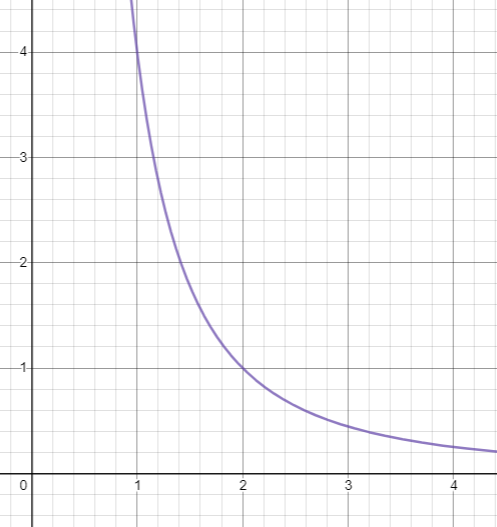
Assume that f is the function defined on the interval [1, 2] by the formula f(x) = 4 / x². Thus the domain of f is the interval [1, 2], the range of f is the interval [1, 4], and the graph of f is shown here.

For each function g described below:

(a) Sketch the graph of g.

(b) Find the domain of g (the endpoints of this interval should be shown on the horizontal axis of your sketch of the graph of g).

(c)  Give a formula for g.

(d) Find the range of g (the endpoints of this interval should be shown on the vertical axis of your sketch of the graph of g).

Solution :

(a)  By shifting the given graph, 1 unit up we get the graph of g.

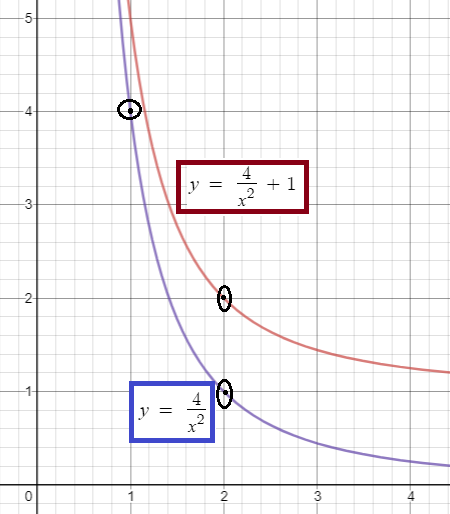
(b) The domain of g is the same as the domain of f . Thus the domain of g is the interval [1, 2].

(c)  Because the graph of g is obtained by shifting the graph of f up 1 unit, we have g(x) = f(x) + 1. Thus

g(x)  =  (4/x²) + 1

for each number x in the interval [1, 2].

(d) The range of g is obtained by adding 1 to each number in the range of f . Thus the range of g is the interval [2, 5].

After having gone through the stuff given above, we hope that the students would have understood "Shifting Graph Up and Down Examples". 

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.