SIMILAR POLYGONS WORKSHEET

Problem 1 :

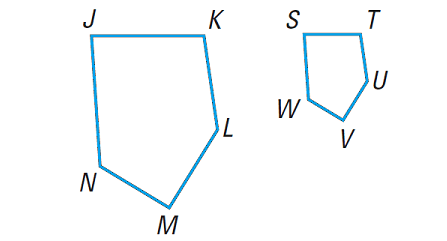
Pentagons JKLMN and STUVW shown below are similar. List all the pairs of congruent angles. Write the ratios of the corresponding sides in a statement of proportionality.

Problem 2 :

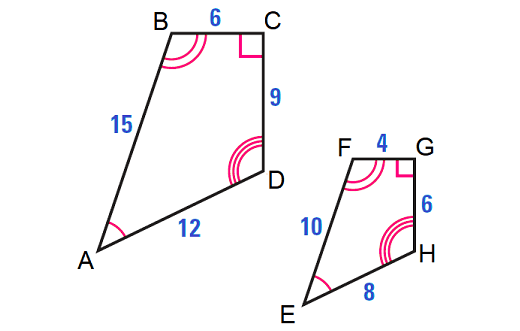
Decide whether the figures are similar. If they are similar, write a similarity statement.

Problem 3 :

We are asked to create a poster to advertise a field trip to see the Liberty Bell. We have a 3.5 inch by 5 inch photo that you want to enlarge. We want the enlargement to be 16 inches wide. How long will it be ?

Problem 4 :

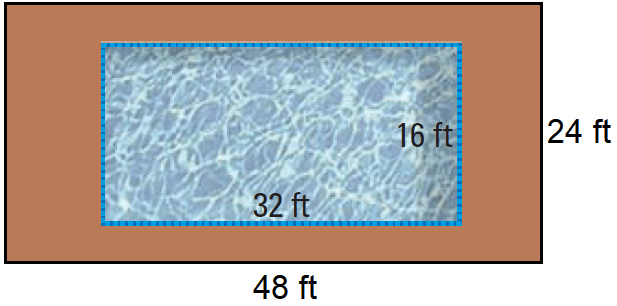
The rectangular patio around a pool is similar to the pool as shown below. Calculate the scale factor of the patio to the pool, and find the ratio of their perimeters.

Problem 5 :

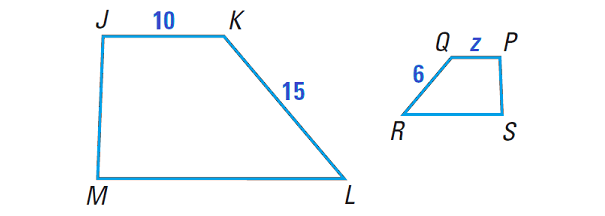
In the diagram shown below, quadrilateral JKLM is similar to quadrilateral PQRS. Find the value of z. 

Answers

1. Answer :

Because JKLM ∼ STUVW, we can write 

∠J ≅ ∠S

∠K ≅ ∠T

∠L ≅ ∠U

∠M ≅ ∠V

∠N ≅ ∠W

We can write the statement of proportionality as follows :

JK/ST = KL/TU = LM/UV = MN/VW = NJ/WS

2. Answer :

As shown, the corresponding angles of ABCD and EFGH are congruent. Also, the corresponding side lengths are proportional. 

AB/EF = 15/10 = 3/2

BC/FG = 6/4 = 3/2

CD/GH = 9/6 = 3/2

DA/HE = 12/8 = 3/2

Hence, the two figures are similar and we can write

ABCD ∼ EFGH

Note :

If two polygons are similar, then the ratio of the lengths of two corresponding sides is called the scale factor. In the above example, the common ratio is 3/2 is the scale factor of ABCD to EFGH.

3. Answer :

To find the length of the enlargement, you can compare the enlargement to the original measurements of the photo.

From the diagram shown above, we have

x/5 = 16/3.5

Multiply both sides by 5.

x = 16/0.7

x ≈ 22.9 in.

Hence, the length of the enlargement will be about 23 inches.

4. Answer :

Because the rectangles are similar, the scale factor of the patio to the pool is 48 : 32, which is 3 : 2 in simplified form.

The perimeter of the patio is

2(24) + 2(48) = 144 feet

and the perimeter of the pool is

2(16) + 2(32) = 96 feet.

The ratio of the perimeters is

= 144/96

= 3/2

In similar figures, the ratio of the perimeters is the same as the scale factor.

So, the scale factor of the patio to the pool is 3/2.

5. Answer :

Because the quadrilaterals JKLM is similar to PQRS, we can set up the proportion that contains PQ.

Write proportion :

KL/QR = JK/PQ

Substitute.

15/6 = 10/z

5/2 = 10/z

Using reciprocal property,

2/5 = z/10

Multiply each side by 10.

2(2) = z

4 = z

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.