SIN COS AND TAN OF SPECIAL ANGLES

There are two types of special triangles. These triangles are 

A 30 - 60 - 90 triangle is a right triangle with a 30° degree angle and a 60° degree angle.

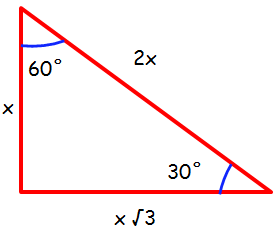
Let x be the length of shorter side. The hypotenuse side is twice as long as the shorter side. The longer side is √3 times as long as shorter side.

By using the above special triangle we can find the values of 30 and 60 degrees all six trigonometric ratios.

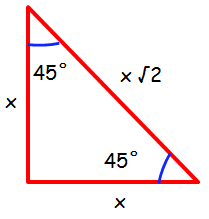
Let x be the length of equal side. The hypotenuse side is  √2 times the length of either side.

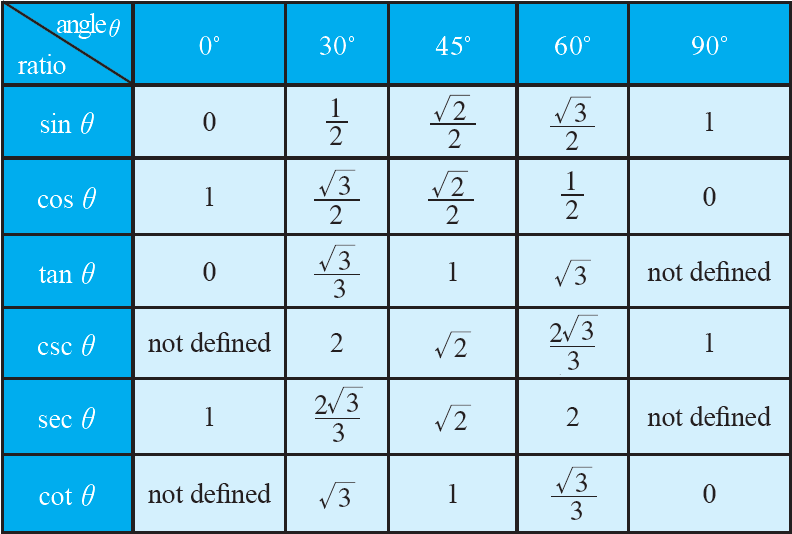
Trigonometric Ratios of 0° and 90°

Consider the figure given below which shows a circle of radius 1 unit centered at the origin.

Let P be a point on the circle in the first quadrant with coordinates (x, y).

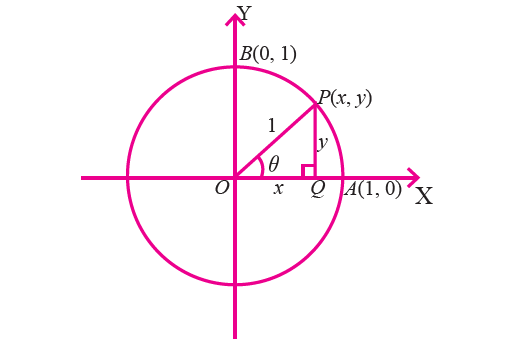
We drop a perpendicular PQ from P to the x-axis in order to form the right triangle OPQ.

Let <POQ  =  θ, then 

sin θ  =  PQ / OP  =  y/1  =  y  (y coordinate of P)

cos θ  =  OQ / OP  =  x/1  =  x  (x coordinate of P)

tan θ  =  PQ / OQ  =  y/x

If OP coincides with OA, then angle θ  =  0°.

Since, the coordinates of A are (1, 0), we have

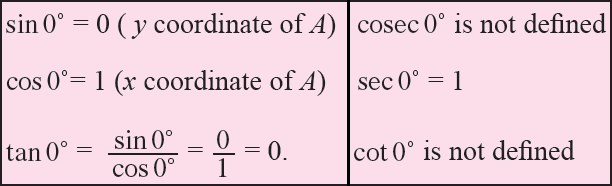
If OP coincides with OB, then angle θ  =  90°.

Because, the coordinates of B are (0, 1), we have

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.