SOLVING ALGEBRAIC FRACTIONS WITH QUADRATICS

Example 1 :

x + [1/(x + 2)]  =  4

Solution :

x + [1/(x + 2)]  =  4

By taking the least common multiple, we get

x(x + 2)/(x + 2) + 1/(x + 2)  =  4

[x(x + 2) + 1]/(x + 2)  =  4

(x² + 2x + 1)/(x + 2)  =  4

By cross multiplication, we get

x² + 2x + 1  =  4(x + 2)

x² + 2x + 1  =  4x + 8

x² + 2x + 1 – 4x – 8  =  0

x² – 2x – 7  =  0

Since this quadratic equation is not factorable, we can solve it using quadratic formula.

x  =  [-b ± √(b² – 4ac)]/2a

Here a  =  1, b  =  -2 and c  =  -7

x  =  [-(-2) ± √(-2)² – 4(1)(-7)]/2(1)

x  =  [2 ± √(4+28)]/2(1)

x  =  [2 ± √(32)]/2

x  =  [2 ± 4√2]/2

x  =  2(1 ± 2√2)/2

x  =  1 ± 2√2

So, the solution of x is 1 ± 2√2.

Example 2 :

3x – [4/(x + 1)]  =  10

Solution :

3x - [4/(x + 1)]  =  10

By taking the least common multiple, we get

3x(x + 1)/(x + 1) - 4/(x + 1)  =  10

[3x(x + 1) - 4]/(x + 1)  =  10

(3x² + 3x - 4)/(x + 1)  =  10

By cross multiplication, we get

3x² + 3x - 4  =  10(x + 1)

3x² + 3x - 4  =  10x + 10

3x² + 3x - 4 – 10x – 10  =  0

3x² – 7x – 14  =  0

This quadratic equation is not factorable. So, we have to use quadratic formula to solve the quadratic equation.

x  =  [-b ± √(b² – 4ac)]/2a

Here a  =  3, b  =  -7 and c  =  -14

x  =  [-(-7) ± √(-7)² – 4(3)(-14)]/2(3)

x  =  [7 ± √(49 + 168)]/6

x  =  (7 ± √217)/6

So, the solution of x is (7 ± √217)/6

Example 3 :

(x + 2)/(x - 1)  =  3x/(x + 1)

Solution :

(x + 2)/(x – 1)  =  3x/(x + 1)

By cross multiplication, we get

(x + 2) (x + 1)  =  3x(x – 1)

x² + x + 2x + 2  =  3x² – 3x

3x² – 3x - x² - x - 2x – 2  =  0

2x² – 6x – 2  =  0

Dividing by 2, we get

x² – 3x – 1  =  0

x  =  [-b ± √(b² – 4ac)]/2a

Here a  =  1, b  =  -3 and c  =  -1

x  =  [-(-3) ± √(-3)² – 4(1)(-1)]/2(1)

x  =  [3 ± √(9 + 4)]/2

x  =  (3 ± √13)/2

So, the solution of x is (3 ± √13)/2

Find x in :

Example 4 :

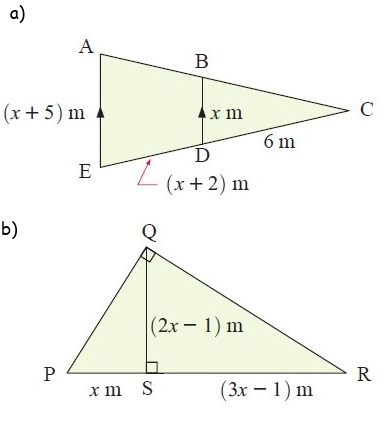
Solution  :

a)

Given BD || AE

<CBD  =  <CAE

<BCD  =  <ACE

By using AA theorem,

∆CBD ~ ∆CAE

Then, BD/AE  =  CD/CE

Here, BD  =  x m, AE  =  (x + 5) m,

CD  =  6 m and CE  =  (x + 8) m

x/(x + 5)  =  6/(x + 8)

By cross multiplication, we get

x(x + 8)  =  6(x + 5)

x² + 8x  =  6x + 30

x² + 2x – 30  =  0

So we have to find x value using the quadratic formula.

x  =  [-b ± √(b² – 4ac)]/2a

Here a  =  1, b  =  2 and c  =  -30

x  =  [-(2) ± √(2)² – 4(1)(-30)]/2(1)

x  =  [-2 ± √(4 + 120)]/2

x  =  (-2 ± √124)/2

x  =  (-2 ± 2√31)/2

 x  =  -1 ± √31

x  =  -1 + √31 and x  =  -1 - √31

So, the value of x is -1 + √31

b)

In right ∆PQR

The perpendicular drawn from the right angle, then the large triangle PQR is similar to the triangles PQS and QSR.

x(3x – 1)  =  (2x – 1)(2x – 1)

3x² – x  =  4x² – 2x – 2x + 1

4x² – 2x – 2x + 1 – 3x² + x  =  0

x² – 3x + 1  =  0

x  =  [-b ± √(b² – 4ac)]/2a

Here a  =  1, b  =  -3 and c  =  1

x  =  [-(-3) ± √(-3)² – 4(1)(1)]/2(1)

x  =  [3 ± √(9 - 4)]/2

x  =  (3 ± √5)/2

x  =  (3 + √5)/2 and x  =  (3 - √5)/2

we are taking it a positive value.

So, the solution of x is (3 + √5)/2

Example 5 :

Two numbers have a sum of 4, and the sum of their reciprocals is 8. Find the numbers.

Solution :

Let the two numbers x and y.

x + y  =  4 -----(1)

1/x + 1/y  =  8 -----(2)

Considering equation (2), we have

1/x + 1/y  =  8

(y + x)/xy  =  8

y + x  =  8xy

By using equation (1), we get

4  =  8xy

1  =  2xy

1  =  2x(4 – x)

1  =  8x – 2x²

2x² – 8x + 1  =  0

Solving this quadratic equation using formula, we get

x  =  [-b ± √(b² – 4ac)]/2a

Here a  =  2, b  =  -8 and c  =  1

x  =  [-(-8) ± √(-8)² – 4(2)(1)]/2(2)

x  =  [8 ± √(64 - 8)]/4

x  =  (8 ± √56)/4

x  =  (8 ± 2√14)/4

x  =  (2 ± 1/2√14)

x  =  (2 + 1/2√14) and x  =  (2 – 1/2√14)

we are taking a positive value.

By applying x  =  (2 + 1/2√14) in equation (1), we get

x + y  =  4

2 + 1/2√14 + y  =  4

y  =  4 – 2 – 1/2√14

y  =  2 – 1/2√14

Then x  =  (2 + 1/2√14) then y  =  2 – 1/2√14.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.