SOLVING EQUATIONS THAT REPRESENT GEOMETRIC CONCEPTS

We can represent geometric relationships using equations.

Recall that a straight line has an angle measure of 180°. Two angles whose measures have a sum of 180° are called supplementary angles.

Two angles whose measures have a sum of 90° are called complementary angles.

Example 1 :

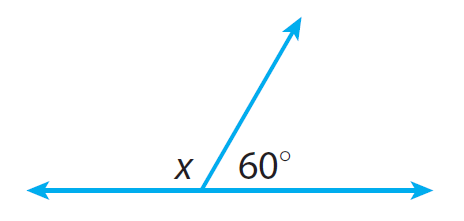
Find the measure of the unknown angle in the figure given below.

Solution :

Step 1 :

Write a word equation based on the situation.

In the given figure, the unknown angle 'x' and the given angle 60° form angle on the straight line.

We know that the angle on the straight line measures 180°. 

So, we have

Step 2 :

Rewrite the equation using a variable for the unknown quantity and the given values for the known quantities.

x + 60°  =  180°

(x represents the measure of the unknown angle in degrees)

Step 3 : 

Solve the equation : x + 60°  =  180°

Since we are trying to solve for "x", we have to get rid of 60° which is added to 'x'.

To get rid of 60°, we have to subtract 60° on both sides. 

(x + 60°) - 60°  =  (180°) - 60°

x  =  120°

So, the unknown angle is 120°.

Example 2 :

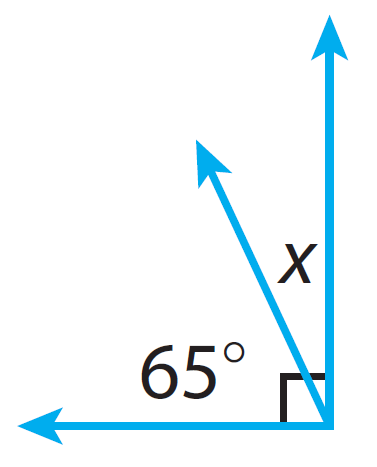
Find the measure of the unknown angle in the figure given below.

Solution :

Step 1 :

Write a word equation based on the situation.

In the given figure, the unknown angle 'x' and the given angle 65° form right angle.

We know that the right angle measures 90°. 

So, we have

Step 2 :

Rewrite the equation using a variable for the unknown quantity and the given values for the known quantities.

x + 65°  =  90°

(x represents the measure of the unknown angle in degrees)

Step 3 : 

Solve the equation : x + 65°  =  90°

Since we are trying to solve for "x", we have to get rid of 65° which is added to 'x'.

To get rid of 65°, we have to subtract 65° on both sides. 

(x + 65°) - 65°  =  (90°) - 65°

x  =  25°

So, the unknown angle is 25°.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.