SOLVING EQUATIONS USING CROSS MULTIPLICATION METHOD

Question 1 :

Solve by cross-multiplication method

(i)  8x − 3y = 12 ; 5x = 2y + 7

Solution :

8x − 3y - 12  =  0  -----(1)

5x - 2y - 7  =  0  -----(2)

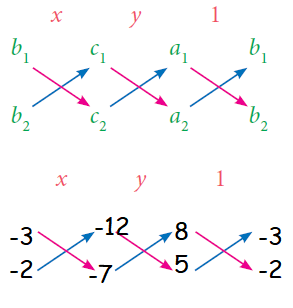
x/(21 - 24)  =  y/(-60 + 56)  =  1/(-16 + 15)

x/(- 3)  =  y/(-4)  =  1/(-1)

x/(-3)  =   -1           y/(-4)  =  -1

x  =  3  and y  =  4

Hence the solution is (3, 4).

(ii)  6x + 7y - 11  =  0; 5x + 2y  =  13

Solution :

6x + 7y - 11  =  0 ------(1)

5x + 2y - 13  =  0 ------(2)

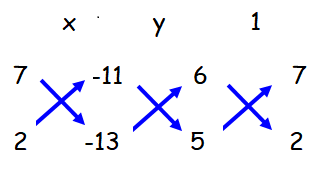
x/(-91 + 22)  =  y/(-55 + 78)  =  1/(12 - 35)

x/(-69)  =  y/(-23)  =  1/(-23)

x  =  -69/(-23)  =  3

y  =  -23/(-23)  =  1

Hence the solution is (3, 1).

(iii)  (2/x) + (3/y)  =  5, (3/x) - (1/y) + 9  =  0

Solution :

Let 1/x  =  a and 1/y  =  b

2a + 3b - 5  =  0 ------------(1)

3a - b + 9  =  0 ------------(2)

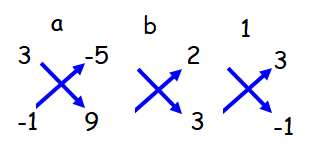
a/(27 - 5)   =  b/(-15 - 18)  =  1/(-2 - 9)

a/(22)   =  b/(33)  =  1/(-11)

a  =  22/(-11)  =  -2, b  =  33/(-11)  =  -3

x  =  -1/2, y  =  -1/3

Hence the solution is (-1/2, -1/3).

Question 2 :

Akshaya has 2 rupee coins and 5 rupee coins in her purse. If in all she has 80 coins totalling ₹ 220, how many coins of each kind does she have.

Solution :

Let "x" and "y"  number of 2 rupee and 5 rupee coins respectively.

x + y  =  80

2x + 5y  =  220

x + y - 80  =  0 ----------(1)

2x + 5y - 220  =  0 ----------(2)

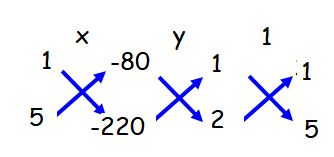
x/(-220 + 400)  =  y/(-160 + 220)  =  1/(5 - 2)

x/(180)  =  y/(60)  =  1/(3)

x  =  180/3, y = 60/3

x  =  60, y = 20

Hence number of 2 rupee coin and 5 rupee coins are 60 and 20 respectively.

Question 3 :

It takes 24 hours to fill a swimming pool using two pipes. If the pipe of larger diameter is used for 8 hours and the pipe of the smaller diameter is used for 18 hours. Only half of the pool is filled. How long would each pipe take to fill the swimming pool.

Solution :

Let x and y be two pipes.

So in 1 hour quantity of water filled by pipe x is 1/x and that of pipe y is 1/y. The quantity of water filled by both pipes in one hour is 1/x + 1/y

It takes 24 hours by pipes to fill the pool

So, 1/x + 1/y = 1/24------------(1)

The quantity of water filled in 8 hours by pipe A = 8/A

The quantity of water filled in 18 hours by pipe B = 18/B

Given in the question half is filled so

 8/x + 18/y = 1/2-------------(2)

From (1) and (2) we have,

a + b - (1/24)  =  0 -------------(3) 

8 a + 18 b - (1/2)  =  0----------(4)

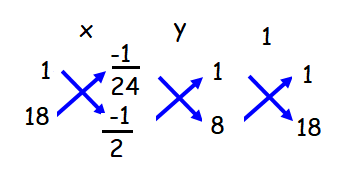
a/(-1/2 + 3/4)  =  b/(-1/3 + 1/2)  =  1/(18 - 8)

a/(-2 + 3)/4  =  b/(-2 + 3)/6)  =  1/(10)

a/(1/4)  =  b/(1/6)  =  1/10

a  =  1/40, b  =  1/60

x  =  40  and y  =  60

Hence larger pipe is taking 40 hours and smaller pipe is taking 60 hours.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.