SOLVING LINEAR SYSTEMS BY ADDING OR SUBTRACTING

We can use elimination method to solve a system of linear equations. In this method, one variable is eliminated by adding or subtracting the two equations of the system to obtain a single equation in one variable.

The following steps will be useful to solve a system of linear equations by subtracting. 

Step 1 :

The variable which is eliminated must have the same coefficient in both the equations. If not, make them to be same using least common multiple and multiplication.

Step 2 :

Add or subtract the equations to eliminate one of the variables.

Step 3 :

Solve the resulting equation for the other variable.

Step 4 :

Substitute the value of the variable received in step 3 into one of the equations to find the value of the variable eliminated in step 2.  

Solved Examples

Example 1 :

Solve the system of equations by adding. Check your the solution by graphing.

2x - 3y  =  12

x + 3y  =  6

Answer :

Step 1 :

In the given two equations, the variable y is having the same coefficient (3). And also, the variable y is having different signs. 

So we can eliminate the variable y by adding the two equations. 

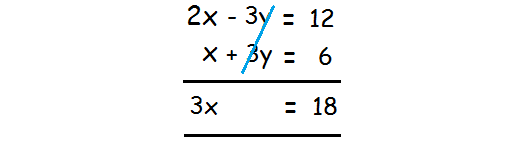
Step 2 :

Solver the resulting equation for the variable x.

3x  =  18

Divide both sides by 3. 

3x / 3  =  18 / 3

x  =  6

Step 3 : 

Substitute the value of x into one of the equations to find the value of y. 

x + 6y  =  6

Subtract 6 from both sides.

aaaaaaaaaaaaaaaaaaaaaa 6 + 3y  =  6 aaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaa  - 6           - 6 aaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaa  -------------- aaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaa          3y  =  0 aaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaa  -------------- aaaaaaaaaaaaaaaaaaa 

Divide both sides by 3

3y / 3  =  0 / 3

y  =  0

Step 3 : 

Write the solution as ordered pair as (x, y). 

(6, 0)

Step 4 : 

Check the solution by graphing. 

To graph the equations, write them in slope-intercept form.

That is, 

y  =  mx + b 

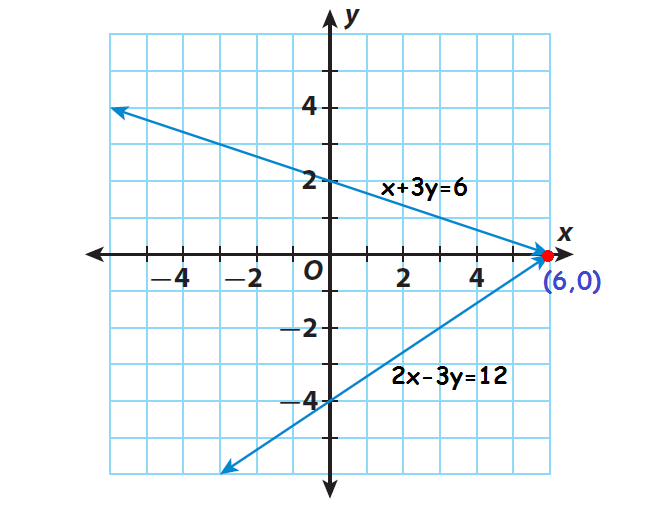
The point of intersection is (6, 0).

Example 2 :

Solve the system of equations by subtracting. Check the solution by graphing.

3x + 3y  =  6

3x - y  =  - 6

Solution :

Step 1 :

In the given two equations, the variable x is having the same coefficient (3), And also, the variable x is having the same sign in both the equations.  

So we can eliminate the variable x by subtracting the two equations.  

(3x + 3y) - (3x - y)  =  (6) - (-6)

3x + 3y - 3x + y  =  6 + 6

Simplify.

4y  =  12

Divide both sides by 4.

4y / 4  =  12 / 4

y  =  3

Step 2 : 

Plug y  =  3 in one of the equations. 

3x - y  =  - 6

3x - 3  =  - 6 

Add 3 to both sides.

(3x - 3) + 3  =  (-6) + 3  

3x - 3 + 3  =  -6 + 3

Simplify.

3x  =  -3

Divide both sides by 3

3x / 3  =  -3 / 3

x  =  - 1

Step 3 : 

Write the solution as ordered pair as (x, y). 

(-1, 3)

Step 4 : 

Check the solution by graphing. 

To graph the equations, write them in slope-intercept form.

That is, 

y  =  mx + b

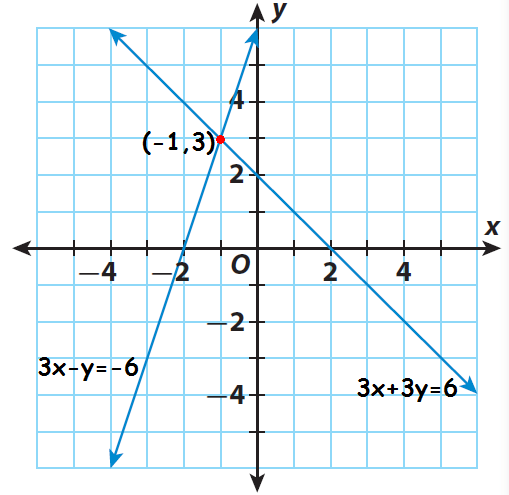
The point of intersection is (-1, 3).

Example 3 :

Sum of the cost price of two products is $50. Sum of the selling price of the same two products is $52. If one is sold at 20% profit and other one is sold at 20% loss, find the cost price of each product.  

Solution :

Step 1 :

Let x and y be the cost prices of two products. 

Then,  

x + y  =  50 -----(1)

Step 2 :

Let us assume that x is sold at 20% profit

Then, the selling price of x is 120% of x.

Selling price of x  =  1.2x

Let us assume that y is sold at 20% loss

Then, the selling price of y is 80% of y.

Selling price of y  =  0.8y

Given : Selling price of x  +  Selling price of y  =  52

1.2x + 0.8y  =  52

To avoid decimal, multiply both sides by 10

12x + 8y  =  520

Divide both sides by 4.

3x + 2y  =  130 -----(2)

Step 3 : 

Eliminate one of the variables to get the value of the other variable.

In (1) and (2), both the variables x and y are not having the same coefficient.

One of the variables must have the same coefficient. 

So multiply both sides of (1) by 2 to make the coefficients of y same in both the equations.  

(1) ⋅ 2 ----->  2x + 2y  =  100 -----(3) 

Variable y is having the same sign in both (2) and (3). 

To change the sign of y in (3), multiply both sides of (3) by negative sign.

- (2x + 2y)  =  - 100

- 2x - 2y  =  - 100 -----(4)

Step 4 : 

Now, eliminate the variable y in (2) and (4) as given below and find the value of x. 

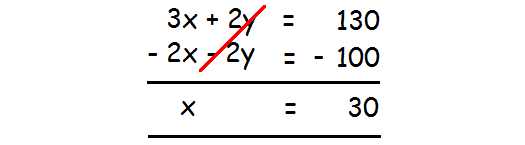
Step 5 : 

Substitute x  =  30 in (1) to get the value of y. 

(2)-----> 30 + y  =  50

Subtract 30 from both sides. 

y  =  20

So, the cost prices of two products are $30 and $20.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.