SOLVING LINEAR SYSTEMS USING MATRICES
The following steps will be useful to solve a system of linear equation using matrices.
Step 1 :
Write the given system of linear equations as matrix.
Example :
Let us consider the following system of linear equations.
2x + 3y = 8
7x - 2y = 3
The above system can be written as a matrix as shown below.
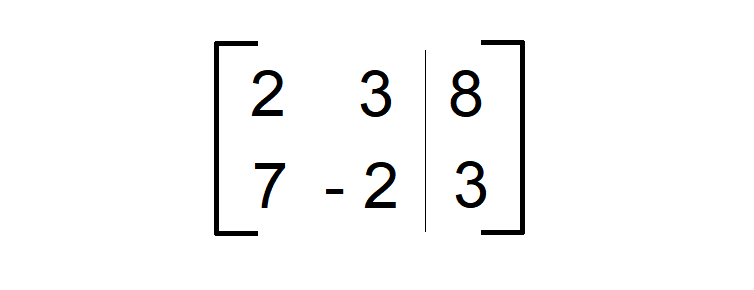
Step 2 :
To solve the given system of linear equations, we have to use row operations and write the above matrix in reduced echelon form.
Reduced row echelon form for the system of two linear equations :

From the above matrix, the solution to the system of two linear equations is (a, b).
Reduced row echelon form for the system of three linear equations :
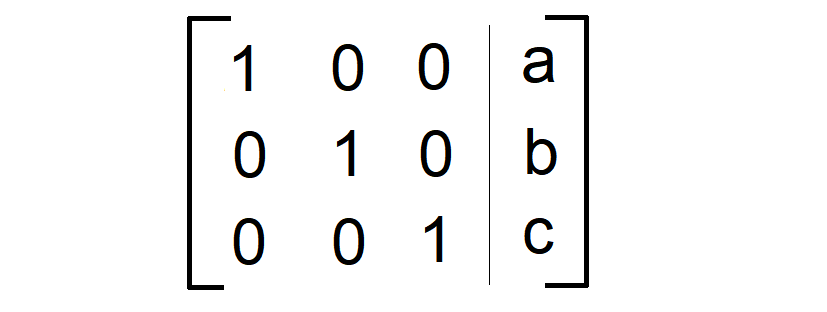
From the above matrix, the solution to the system of three linear equations is (a, b, c).
Row Operations
Row operations can be applied to create an equivalent matrix.
There are three basic row operations.
1.Switching Rows :
Switching rows allows you to switch a row with another row.
Example :
Switching the first row with the second row.
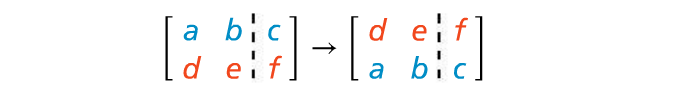
2.Multiplication and Division :
Multiply or divide elements of a row by a nonzero constant.
Example :
* Multiply the first row by 3.
* Multiply the second row by 1/2, which is equivalent to dividing by 2.
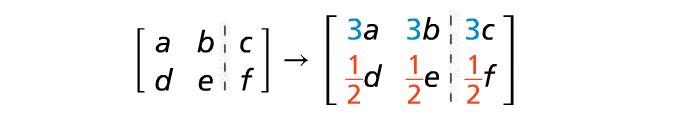
3.Addition and Subtraction :
Add elements of a row to (or subtract them from) elements of another row. This produces a new row, which you can use to replace one of the two rows you just combined.
Example :
Subtract the second row from the first row, replacing the first row with the difference.
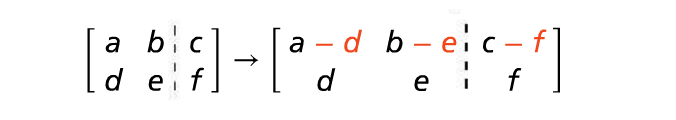
Solved Examples
Example 1 :
Solve the system of linear equations given below using matrices.
x - 2y = 25
2x + 5y = 4
Solution :
Write a matrix representation of the system of equations.
|
Each equation corresponds to a matrix now |
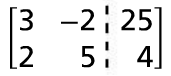 |
To solve a linear system of equations using a matrix, analyze and apply the appropriate row operations to transform the matrix into its reduced row echelon form.
|
Multiply the first row by 2 and second row by 3. |
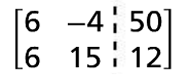 |
|
Replace the first row with r1 - r2. Divide the second row by 3. |
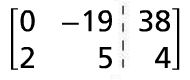 |
|
Divide the first row by -19. |
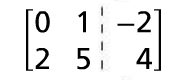 |
|
Multiply the first row by -5. |
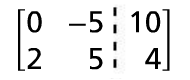 |
|
Replace the second row with r1 + r2. |
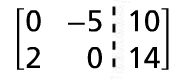 |
|
Divide the first row by -5 and the second row by 2. |
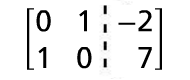 |
|
Switch the first row and second row. |
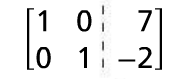 |
The final matrix is in reduced row echelon form and it allows us to find the values of x and y.
Hence, the solution of the system of linear equations is
(7, -2)
That is,
x = 7 and y = - 2
Justification :
Check that the values x = 7 and y = -2 satisfy both the equations.

Example 2 :
Solve the system of linear equations given below using matrices.
x + y + 2z = 13
2y + z = 5
2x - y = 6
Solution :
Write a matrix representation of the system of equations.
|
Each equation corresponds to a matrix now |
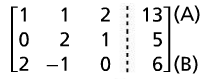 |
As we have done in example 1, apply the appropriate row operations to transform the matrix into its reduced row echelon form.
|
(B) - 2(A) becomes (D) |
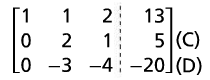 |
|
(D) + 4(C) becomes (E) |
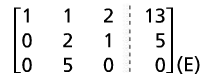 |
|
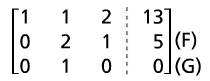
(E) divided 5 becomes (G) |
 |
|
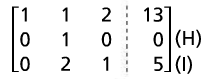
Switch (G) and (F). Now (H) matches reduced row echelon form. |
 |
|
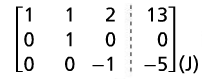
2(H) - (I) becomes (J) |
 |
|
Multiply (J) by -1. Now (M) matches the reduced row echelon form. |
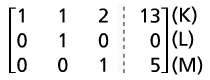 |
|
(K) - (L) becomes (N) |
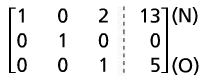 |
|
(N) - 2(O) becomes (P). |
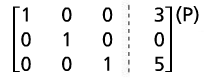 |
The final matrix is in reduced row echelon form and it allows us to find the values of x, y and z.
Hence, the solution of the system of linear equations is
(3, 0, 5)
That is,
x = 3, y = 0 and z = 5
Justification :
Check that the values x = 3 and y = 0 and z = 5 satisfy the given system of linear equations.
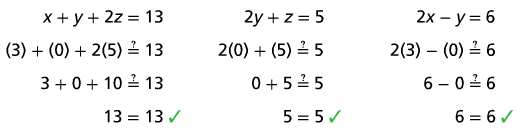
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Word Problems on Division
Nov 17, 24 01:42 PM
Word Problems on Division -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Nov 16, 24 08:15 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 71)
Nov 16, 24 08:03 AM
Digital SAT Math Problems and Solutions (Part - 71)