SOLVING QUADRATICS REAL AND IMAGINARY SOLUTIONS

Find roots of the quadratic equations given below.

Example 1 :

x² - 6x + 12 = 0

Solution :

x²-6x+12  =  0

a  =  1, b  =  -6 and c  =  12

Solving the quadratic equation using the formula

x  =  -b±√(b²-4ac)/2a

we can solve the equation.

b²-4ac  =  6² - 4 ⋅ 1 ⋅ 12

=  36 - 48

=  -12 < 0

Since b²-4ac < 0, the quadratic equation will have imaginary roots.

√b²-4ac  =  √-12  ==>  2i√3

x  =  (6 ± 2i√3)/2

x  =  (3 ± i√3)

So, the roots are 3 + i√3 and 3 - i√3.

Example 2 :

14 - 3x²  =  2x

Solution :

14-3x²  =  2x

Multiply by negative.

3x² - 14  =  -2x

3x²+2x-14  =  0

a  =  3, b  =  2 and c  =  -14

Solving the quadratic equation using the formula

x  =  -b±√(b²-4ac)/2a

we can solve the equation.

b²-4ac  =  2² - 4 ⋅ 3 ⋅ (-14)

=  4 + 168

=  172 > 0

Since b²-4ac > 0, the quadratic equation will have real roots.

√b²-4ac  =  √172  ==>  2√43

x  =  (2 ± 2√43)/2

x  =  (1 ± √43)

So, the roots are (1+√43)/2 and (1-√43)/2.+

Find a possible pair of integer values for a and c so that the quadratic equation has the given solution(s). 

Example 3 :

ax² + 4x + c = 0 has two imaginary solution.

Solution :

Since the quadratic equation has imaginary roots.

b²-4ac < 0

a  =  a, b  =  4 and c  =  c

4²-4ac < 0

16-4ac < 0

To  get the imaginary  solutions, 4ac should be > 16

So, product of a and c should be > 4

One of the possible value If a  =  2 and b  =  3

So, the required equation is 2x² + 4x + 3 = 0

Example 4 :

 ax² − 8x + c = 0 two real solutions

Solution :

Since the quadratic equation has imaginary roots.

b²-4ac > 0

a  =  a, b  =  -8 and c  =  c

(-8)²-4ac > 0

64-4ac > 0

To  get the real solutions, 4ac should be > 64

So, product of a and c should be < 16

One of the possible value If a  =  2 and b  =  3

So, the required equation is 2x² − 8x + 3 = 0

Example 5 :

Use the discriminant of f(x) = 0 and the sign of the leading coefficient of f(x) to match each quadratic function with the graph.

Explain your reasoning. Then find the real solution (s) if any each quadratic equation f(x) = 0.

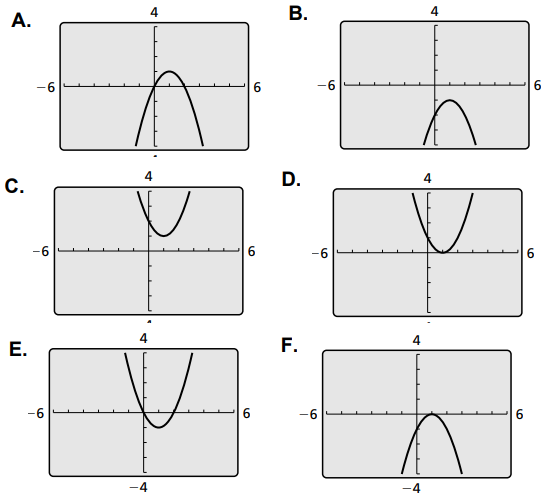
1)  f(x) = x² - 2x

2)  f(x) = x² - 2x + 1

3)  f(x) = x² - 2x + 2

4)  f(x) = -x² + 2x

5)  f(x) = -x² + 2x - 1

6)  f(x) = -x² + 2x - 2

Solution :

1)  f(x) = x² - 2x

Let f(x) = 0

x² - 2x = 0

x(x - 2) = 0

x = 0 and x = 2

The parabola should intersect the x-axis at two different points 0 and 2.

Direction of opening of parabola : Open upward.

So, graph E is the correct graph for the function f(x) = x² - 2x.

2)  f(x) = x² - 2x + 1

Let f(x) = 0

x² - 2x + 1 = 0

(x - 1)(x - 1) = 0

x = 1 and x = 1

The parabola should touch the x-axis at a point 1.

Direction of opening of parabola : Open upward.

So, graph D is the correct graph for the function f(x) = x² - 2x + 1.

3)  f(x) = x² - 2x + 2

Let f(x) = 0

x² - 2x + 2 = 0

Finding discriminant :

Δ = b²-4ac

a = 1, b = -2 and c = 2

= (-2)²- 4 (1) (2)

= 4 - 8

= -8 < 0

So, the quadratic equation doesn't have real roots, it has imaginary roots.

The parabola should not touch the x-axis.

Direction of opening of parabola : Open upward.

So, graph C is the correct graph for the function f(x) = x² - 2x + 2.

4)  f(x) = -x² + 2x

Let f(x) = 0

-x² + 2x = 0

-x(x - 2) = 0

x = 0 and x = 2

The parabola should intersect the x-axis at two different points 0 and 2.

Direction of opening of parabola : Open downward

So, graph A is the correct graph for the function

f(x) = -x² + 2x

5)  f(x) = -x² + 2x - 1

Let f(x) = 0

-x² + 2x - 1 = 0

Multiplying by negative, we get

x² - 2x + 1 = 0

(x - 1)(x - 1) = 0

x = 1 and x = 1

The parabola should touch the x-axis at a point x = 1.

Direction of opening of parabola : Open downward.

So, graph F is the correct graph for the function f(x) = -x² + 2x - 1

6)  f(x) = -x² + 2x - 2

Let f(x) = 0

-x² + 2x - 2 = 0

Finding discriminant :

Δ = b²-4ac

a = -1, b = 2 and c = -2

= 2²- 4 (-1) (-2)

= 4 - 8

= -4 < 0

So, the quadratic equation doesn't have real roots, it has imaginary roots.

The parabola should not touch the x-axis.

Direction of opening of parabola : Open downward.

So, graph B is the correct graph for the function

f(x) = -x² + 2x - 2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.