SOLVING SYSTEMS OF EQUATIONS GRAPHICALLY

Instead of solving a system of linear equations using the methods like elimination, substitution and cross-multiplication , we can also solve the system graphically.

To solve the system of linear equations graphically, we have to sketch the graph of each equation. 

The point at which the graphs of the linear equations (straight lines) intersect is the solution of the given system of equations.

The x and y coordinates in the point of intersection are the values of x and y respectively. 

For example, if(a, b) is the point of intersection, 'a' is the value of x and 'b' is the value of y. 

That is. 

x  =  a

y  =  b

Let us look at some examples to understand how to solve system of linear equations graphically. 

Example 1 :

Solve the following system of equations by graphically. 

x + y - 4  =  0

3x - y  =  0

Solution :

Step 1 :

Let us re-write the given equations in slope-intercept form  (y = mx + b). 

y  =  - x + 4

(slope is -1 and y-intercept is 4) 

y  =  3x 

(slope is 3 and y-intercept is 0) 

Based on slope and y-intercept, we can graph the given equations. 

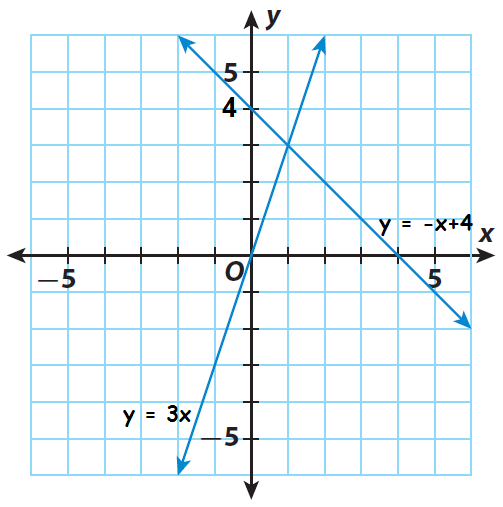
Step 2 :

Find the point of intersection of the two lines. It appears to be (1, 3). Substitute to check if it is a solution of both equations.

Because the point (1, 3) satisfies both the equations, the solution of the system is (1, 3).  

Example 2 :

Solve the following system of equations by graphically. 

3x - y - 3  =  0

x - y - 3  =  0

Solution :

Step 1 :

Let us re-write the given equations in slope-intercept form. 

y  =  3x - 3

(slope is 3 and y-intercept is -3) 

y  =  x - 3 

(slope is 1 and y-intercept is -3) 

Based on slope and y-intercept, we can graph the given equations. 

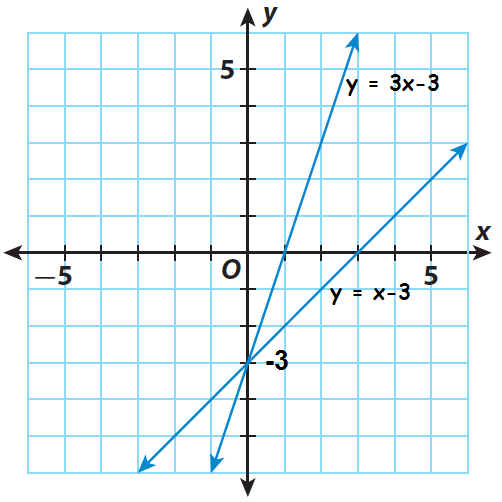
Step 2 :

Find the point of intersection of the two lines. It appears to be (0, -3). Substitute to check if it is a solution of both equations.

Because the point (0, -3) satisfies both the equations, the solution of the system is (0, -3).  

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.