SOLVING SYSTEMS OF EQUATIONS USING INVERSE MATRICES WORKSHEET

(1)  Solve the following system of linear equations by matrix inversion method:

(i)  2x + 5y = -2, x + 2y = -3     Solution

(ii)  2x - y = 8, 3x + 2y = -2          Solution

(iii)  2x + 3y - z = 9, x + y + z = 9, 3x - y - z = -1

Solution

(iv)  x + y + z - 2 = 0, 6x - 4y + 5z - 31 = 0, 5x + 2y + 2z =13

Solution

(2)  If

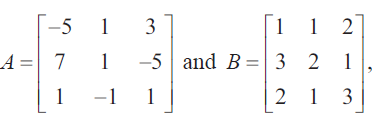
find the products AB and BA and hence solve the system of equations x + y + 2z =1,3x + 2y + z = 7,2x + y + 3z = 2.

Solution

(3)  A man is appointed in a job with a monthly salary of certain amount and a fixed amount of annual increment. If his salary was ₹19,800 per month at the end of the first month after 3 years of service and ₹23,400 per month at the end of the first month after 9 years of service, find his starting salary and his annual increment. (Use matrix inversion method to solve the problem.)       Solution

(4)  Four men and 4 women can finish a piece of work jointly in 3 days while 2 men and 5 women can finish the same work jointly in 4 days. Find the time taken by one man alone and that of one woman alone to finish the same work by using matrix inversion method.      Solution

(5)  The prices of three commodities A,B and C are ₹ x, y and z per units respectively. A person P purchases 4 units of B and sells two units of A and 5 units of C . Person Q purchases 2 units of C and sells 3 units of A and one unit of B . Person R purchases one unit of A and sells 3 unit of B and one unit of C . In the process, P,Q and R earn ₹ 15,000, ₹ 1,000 and ₹4,000 respectively. Find the prices per unit of A,B and C . (Use matrix inversion method to solve the problem.)          Solution

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.